
- •Экзамен по начертательной геометрии
- •1. Метод проецирования. Центральное и параллельное проецирование.
- •2. Чертеж точки в сне теме прямоугольных координат. Способы
- •3. Прямая линия общего и частного положения на эпюре
- •4. Следы прямой линии. Сформулировать последовательность построения горизонтальною и фронтального следов прямой.
- •5. Определение истинной величины отрезка прямой общего положения способом прямоугольного треугольника.
- •6. Взаимное положение точки и прямой, двух прямых. Определение видимости проекций точек на скрещивающихся прямых.
- •8. Горизонтали и фронтали плоскости. Точка и прямая в плоскости.
- •9. Взаимное положение прямой и плоскости (прямые параллельные и перпендикулярные плоскости). Проецирование прямого угла.
- •10. Взаимное положение двух плоскостей. Построение линии пересечения плоскостей при различных способах их задания.
- •11. Правила построения точки пересечения прямой с плоскостью. Определение видимости прямой.
- •12. Аксонометрические проекции. Основные понятия и определения. Построение окружности в аксонометрических проекциях.
- •13. Стандартные виды аксонометрических проекций. Коэффициенты искажения. Построение окружности в аксонометрических проекциях.
- •15. Способ замены плоское! ей.
- •16. Способ врящсния вокруг проецирующих прямых.
- •18. Развертки поверхностен. Развертывание поверхности многогранников.
- •19. Пересечение кривых поверхностей плоскостью частною положения. Линии конических сечений.
- •24. Линейчатые поверхности (развертываемые и неразвертываемые). Нелинейчатые поверхности.
- •26. Построение линии взаимною пересечения многогранных поверхностей.
- •29.Особые случаи пересечения поверхностей вращения.
- •30. Построение .Пшии персе', чения поверхностей способом концентрических вспомогательных
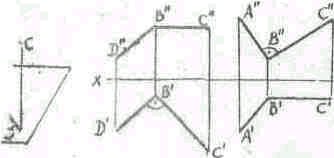
10. Взаимное положение двух плоскостей. Построение линии пересечения плоскостей при различных способах их задания.
...е плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикуляр-.ругой плоскости, или перпендикулярна к прямой, лежащей в другой плоскости.
Две плоскости пересекаются по прямой. В зависимости от, того какое положение занимают плоскости, возможно три случая пересечения плоскостей:
1) Две плоскости занимают частное положение. Возможно два варианта: 1) две пересекающиеся плоскости перпендикулярны к одной плоскости проекций =^> линия пересечения перпендикулярна к этой же плоскости проекций; 2) две пересекающиеся плоскости перпендикулярны к разным плоскостям проекций => линия пересечения есть линия, проекция которой совпадает со следами плоскостей.
2) Одна из плоскостей занимает общее положение, а другая — частное => одна проекция линии пересечения совпадает со следом плоскости частного положения, а другая проекция определяется из условия принадлежности этой прямой плоскости общего положения.
3) Две плосюости занимают общее положение. Построение линии пересечения плоскостей при различных способах их задания:
•^ Провести вспомогательную плоскость, пересекающую две данных плоскости ( плоскость частного положения);
•^ Определить линии пересечения вспомогательных плоскостей с каждой из данных плоскостей;
•^ Найти точки пересечения Полученных линий и соединить их.

11. Правила построения точки пересечения прямой с плоскостью. Определение видимости прямой.
Правила построения точки пересечения прямой с плоскостью:

- Определить линию пересечения заданной и вспомогательной ' плоскостей;
' - Определить точку пересечения прямой с плоскостью как результат заданной прямой с найденной точкой пересечения;
- Определить видимость прямой.
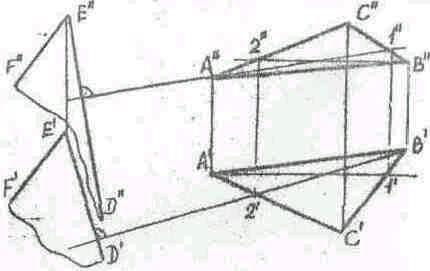
12. Аксонометрические проекции. Основные понятия и определения. Построение окружности в аксонометрических проекциях.
| Способ аксонометрического проецирования заключается в том, что проецирующую фигуру соотносят с некоторой системой прямоугольных координат и вместе с этой системой параллельно проецируют на одну плоскость проекций. Прямые OX, OY, OZ — оси координат в пространстве, прямые ОцХ, OyY, OyZ — их проекции на

проекции отрезка /. Отношения l^ll, /y/Z, 1^11 называются коэффициентами искажения по аксонометрическим осям. Коэффициенты искажения по оси ОуХ обозначим k, по оси o(^y — m, по оси O^Z — п. В зависимости or соотношения коэффициентов искажения проекции делятся на : изометрическую (k=m=n), димегрическую (1<^пт=п), триметрическую (k^m^n). В зависимости от угла между направлением проецирования и аксонометрической плоскостью аксонометрические проекции могут быть косоугольными и прямоугольными.
