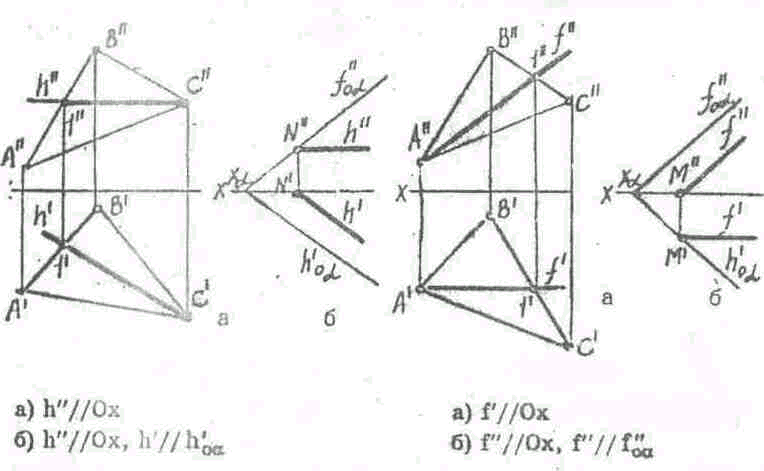
8. Горизонтали и фронтали плоскости. Точка и прямая в плоскости.

Точка принадлежит плоскости,если она лежит на прямой, принадлежащей плоскости. Например, точка D(D',D") принадлежит плоскости АВС (A'B'C', A"B"C"), т. к. она лежит на прямой С1(С'1',С"1"). Прямая принадлежит плоскости, если две ее точки принадрежат плоскости. Прямая принадлежит плоскости,если она проходит через одну точку этой плоскости и параллельна какой-нибудь прямой, лежащей в плоскости. К числу прямых, которые занимают особое положение в плоскости, относят горизонтали и фронтали. Горизонталями плоскости называют прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций. Фронталями плоско­сти называют прямые, принадлежащие плоскости и параллельные фронтальной плоскости проекций.

9. Взаимное положение прямой и плоскости (прямые параллельные и перпендикулярные плоско­сти). Проецирование прямого угла.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, принадлежащей данной плоскости. Прямая перпендикулярна к плоскости, если она перпендикулярна ко всем двум прямым, ко­торые пересекаются в этой плоскости принадлежат ей. Но, чтобы при этом проекция перпендикуляра к плоскости общего положения оказалась перпендикулярной к соответственной проекции некоторой пря­мой этой плоскости- прямая должна быть горизонталью или фронталью, или профильной прямой плос­кости. Поэтому, если надо построить перпендикуляр к плоскости, берут в общем случае две такие пря­мые. Таким образом, у перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проек­ции фронтали. Очевидно, если плоскость задана следами, мы получаем следующий результат: если прямая перпендикулярна к плоскости, то горизонтальная проекция этой прямой перпендикулярна гори­зонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальному следу плоско­сти. Если через точку D надо провести прямую L (Г, I"), перпендикулярную к плоскости, заданой Д АВС нужно выполнить следующие построения:

1) Провести в плоскости горизонталь С1 (СТ, С"1") и фронталь А2 (А'2', А"2");

2) Через горизонтальную проекцию D' точки D провести прямую Г, перпендикулярную к горизонтальной проекции горизонтали СТ, — это будет горизонтальная проекция перпендикуляра;

3) Через фронтальную проекцию D" точки D провести прямую I", перпендикулярную к

фронтальной проекции фронтали А"2", — фронтальная проекция перпендикуляра. Построенная прямая L (Г, I") и есть перпендикуляр к плоскости Д АВС. На основании перпендикулярности прямой и плоскости можно решать следующие задачи: определять расстояние в пространстве; определять расстояние между двумя параллельными плоскостями; прово­дить плоскость, параллельную данной, находящейся на некотором расстоянии; из точки, лежащей в плоскости, строи ть перпендикуляр к ней; проводить через точку плоскость, перпендикулярную к дан­ной плоскости.

Теоретической основой для построения на чертежах проекций прямых и плоскости, перпендикулярных относительно к друг другу, служит теорема о проецировании прямого угла. В общем случае угол про­ецируется на плоскость в натуральную величину, если две его стороны параллельны этой плоскости. Прямой угол проецируется в натуральную величину, если хотя бы одна его сторона параллельна плос­кости проекций, а другие не перпендикулярны к этой плоскости. Таким образом, возможно три случая проецирования прямого угла на плоскость:

1) Если две стороны прямого угла заданы прямыми общего положения, то прямой угол проециру­ется с искажением на все три плоскости проекций;

2) Если две стороны прямого угла параллельны какой-нибудь плоскости проекций, то на эту плос­кость прямой угол проецируется в натуральную величину;

3) Если одна сторона прямого угла прямая общего положения, а другие параллельны плоскости проекций, то прямой угол проецируется на эту плоскость проекций в прямой.