Глава 3. Гармоническая модель собаки, золотое сечение

3.1. Золотое сечение

Тему гармонии собаки мы начнем с разговора о строении произвольной абстрактной формы ее гармонии и образующих ее принципах. Принято рассматривать два таких принципа.

3.1.1. Принцип деления целого в равном отношении

ПЕРВЫМ мы назовем ПРИНЦИП ДЕЛЕНИЯ ЦЕЛОГО В РАВНОМ ОТНОШЕНИИ, простейшим примером которого может служить отрезок, поделенный пополам. Середину этого отрезка может указать безошибочно практически любой человек, из чего следует, что глаз человека от природы настроен на равновесие. Очевидно, что этому принципу соответствуют формы, обладающие симметрией различного рода. Эти формы в силу равенства их частей наделены равновесием и поэтому выглядят законченно статично. Однако гармония произвольной формы не может быть исчерпана действием первого принципа, т.к. эта форма в общем случае предназначена для выполнения какой-то работы, невозможной без движения, в то время как первый принцип закладывает только равновесие в образуемые им формы, и движения они не содержат. Из этого следует, что должен существовать другой принцип, ответственный за гармонию формы, способной к движению.

3.1.2. Принцип деления отрезка в среднегармоническом отношении

Такой ВТОРОЙ формообразующий принцип существует и носит название «ЗОЛОТОГО СЕЧЕНИЯ». Ему соответствует деление отрезка в особенном отношении, оно отличается необычным свойством частей: будучи неравными, они образуют парадоксальное равновесие составляемого ими целого, рождают ощущение совершенства этого «неравновесного» равновесия, возникшего под действием, казалось бы, простой и вместе с тем, необычайной пропорции, воспринимаемой людьми художественно чуткими как некий дар свыше, – не случайно божественной была названа эта пропорция в эпоху Ренессанса. Проиллюстрируем эту мысль на примере человеческого тела, которое, обладая продольной симметрией, в поперечном отношении асимметрично (рис. 121).

Рис. 121. Человеческое тело, обладая продольной симметрией, в поперечном отношении асимметрично

Однако асимметрия верхней и нижней частей при ИЗВЕСТНОМ их соотношении способна создать законченную гармонию, в результате которой составляющие ее НЕРАВНЫЕ части образуют то самое парадоксальное РАВНОВЕСИЕ. Для этого горизонтальная линия, проведенная через пупок, должна разделить тело в отношении золотого сечения. Самым удивительным является то обстоятельство, что художественно одаренные люди, не знакомые ни с фактом существования такого отношения, ни с числом, его выражающим, инстинктивно скажут, насколько хороши пропорции тела и ног конкретного человека. Это означает, что человеческий глаз от природы настроен и на это парадоксальное равновесие. Для ответа на вопрос о том, каким числом выражается золотое сечение, нам придется обратиться к ЕВКЛИДУ (III век до н.э.), давшему ему первоначальное название «деление отрезка в среднегармоническом отношении», хотя сам принцип был уже известен Пифагору (V век до н.э.), а еще раньше египтянам.

3.1.3. Определение евклида

Отрезок называется разделенным в среднегармоническом отношении, если его большая часть относится к меньшей так же, как весь отрезок относится к своей большей части (рис. 122). Это приводит к появлению пропорции: 1:Х = Х:(1-Х).

Положительный корень соответствующего квадратного уравнения соответствует координате искомой точки. Обычно пользуются его приближенным значением 0,618 для определения длины большей части отрезка, тогда на долю меньшей части приходится 0,382.

Рассеченный в этом отношении отрезок отличается названным выше свойством – особенной соразмерностью своих трех частей – меньшей, большей и целого, воспринимаемых глазом как внутренне уравновешенных. Вслушаемся в название этого принципа по Евклиду: деление отрезка в среднегармоническом отношении. Тема гармонии уже тогда, за 3 века до нашей эры, с очевидностью была обнаружена, правда, пока еще в одномерном пространстве – на прямой.

Оказалось, что и при выходе в пространство большей размерности принцип, указанный Евклидом, по-прежнему создает гармоничное целое, если трехчастность его формы подчиняется действию евклидовой пропорции.

Мы уже упомянули пример хорошо сложенного человека, у которого горизонтальная линия, проведенная через пупок, отвечает среднегармоническому сечению. Это давало скульпторам и художникам один из гармонических канонов для определения правильных продольных пропорций человеческого тела. Впоследствии выяснилось, что идеальное строение человека и в целом, и в деталях подчиняется евклидову числу и соответствует классическим представлениям о красоте (Фидий, и в честь его Ф = 1 /X, где X – число Евклида).

Рис. 122. Отрезок называется разделенным в среднегармоническом отношении, если его большая часть относится к меньшей так же, как весь отрезок относится к своей большей части

Рис. 123. Форма головы воспринимается художником совершенной, ест отношение ее поперечного и продольного диаметров в точности соответствует Евклидову числу

Приведем отдельные примеры.

Форма головы воспринимается художником совершенной, если отношение ее поперечного и продольного диаметров в точности соответствует евклидову числу (вспомним овал лица, который есть не что иное, как продольное сечение яйца, рис. 123).

Канон женской красоты (рис. 124) определяется отношением талии к бюсту, равным отношению талии к бедрам и равным числу Евклида.

Канон мужской красоты (рис. 125) определяется этим же числом по-другому: здесь евклидовой пропорции соответствует отношение ширины в бедрах к ширине в плечах.

Внимательный читатель сразу усмотрит в этом проявление полового диморфизма и найдет соответствующее функциональное объяснение.

Оказывается, что под действие евклидова сечения подпадает не только гармония человека: всемирно известные архитектурные строения своими пропорциями также повторяют это число (пирамиды Хеопса, Хефрена и Микерина, Парфенон, театр Диониса в Афинах, церковь Покрова на Нерли, храм Василия Блаженного, церковь Вознесения в Коломенском, система «Модулор» Ле Корбюзье...), ему соответствуют примеры из самых неожиданных областей, о которых мы расскажем позже.

И во всех воплощениях, живых и неживых, форма, рождаемая принципом Евклида, вызывает ощущение

И во всех воплощениях, живых и неживых, форма, рождаемая принципом Евклида, вызывает ощущение гармонии, содержащей в себе внутреннее движение, гармонии напряженной, являющейся антиподом гармонии покоя. Таким образом, наряду с буквальной законченностью симметричной формы и ее статичным равновесием возникает парадоксальная завершенность внутренне напряженной формы, сбалансированность частей которой определяется принципом среднегармонического сечения.

Рис. 124. Канон женской красоты определяется отношением талии к бюсту, равным отношению талии к бедрам и равным числу Евклида

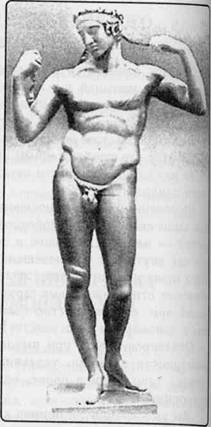
Рис. 125. Канон мужской красоты определяется по-другому: здесь Евклидовой пропорции соответствует отношение ширины в бедрах к ширине в плечах,