Фазовая плоскость.

(1)

j=1,2;

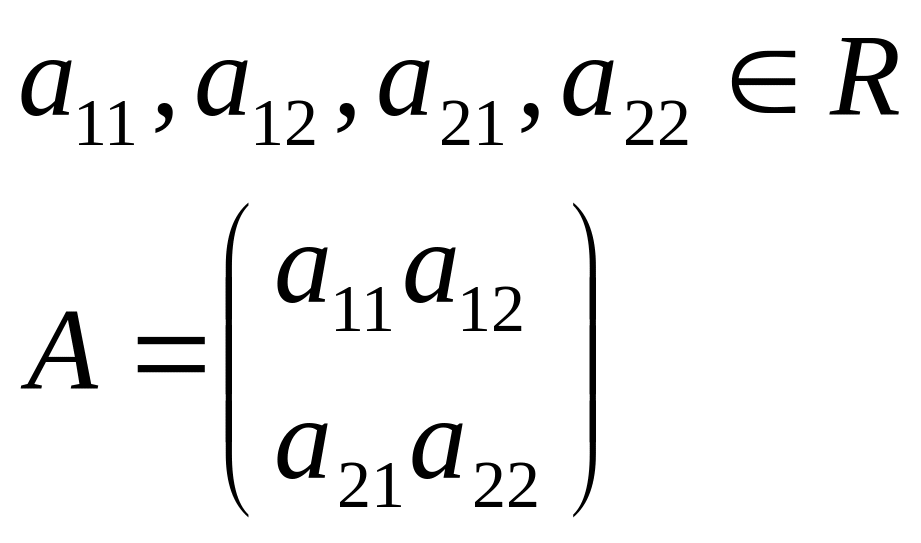
Определения:

1. Фазовой плоскостью называется пространство R² переменных y₁,y_2.

2. Фазовой траекторией называется проекция любой интегральной системы (1) на фазовую плоскость.

3. Фазовой картиной системы (1) называется совокупность всех ее фазовых траекторий.

- собственные значения матрицы A.

Существует 9 типов фазовых картин:

№ п/п	условия	название	краткие пояснения	Схематический рисунок
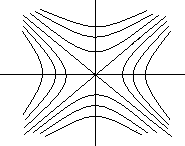
1	sign = =sign	седло	вначале следует провести 2 прямые(сепаратрисы) через нач. координат в направлении собственных векторов , фазовыми траекториями будут 4 семейства кривых в виде сепаратрисы, а также половинки сепаратрис, разграниченных осями координат.
2	sign = sign	узел	проводится 2 сепаратрисы, строятся 2 семейства кривых(параболы), касающихся в нач. координат той сепаратрисы, которой соответствует наименьшее по модулю собственное значение матрицы A.Фазовые траектории – половинки сепаратрис, разграниченные началом координат.
3	Re Im	фокус	фазовые траектории –кривые, типа логарифмических спиралей.	бесконечное мн-во лог, спиралей
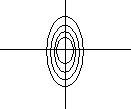
4	Re Im	центр	Фазовая траектория-семейство эллипсов с центром в начале координат, похожие на концентрические окружности.
5		Параллельные полупрямые	Вначале следует провести сепаратрису, в направлении вектора, которому отвечает нулевое собственное значение. Провести семейство прямых, параллельно тому вектору, которому отвечает нулевое значение. Фазовые траектории- точки на сепаратрисах, половинки прямых, разграниченных сепаратрисами.
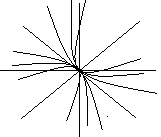
6	У матрицы A 2 линейно независимых собственных вектора.	Дикритический узел	Фазовые траектории- лучи, выходящие из начала координат.
7	1 линейно независимый вектор.	Вырожденный узел	Провести сепаратрису через начало координат в направлении собственного вектора, затем семейство характерных кривых, касающихся в начале координат сепаратрис и симметричных относительно начала координат. Фазовые траектории- половинки сепаратрис и указанных кривых.
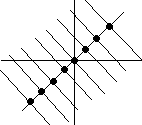
8	1 лин. незав. собств. вектора	Параллельные прямые	Проводят сепаратрисы (как в 1). Фазовые траектории- точки на сепаратрисах и все прямые параллельные сепаратрисам.
9		Всевозможные точки	Фазовые траектории- все точки на фазовой плоскости.

Решение такого вида:

фиксированного

Доказательство для дикритического узла:

2 линейно независимых собственных вектора матрицы A.

Если :

Если :

Линейные интегральные уравнения 2-го рода.

Определение: Интегральным уравнением называется уравнение, содержащее подынтегральную среднюю под интегралом.

Интегральные уравнения:

(1)

K(x, t) - ядро уравнения

F(x) - свободный член (правая часть уравнения)

- параметр (действительное число в общем виде)

Если левая часть обозначается через L(y), то L(y)- линейный оператор.

- однородное, - неоднородное.

Будем полагать все функции в (1) непрерывными.

Нет способа решения уравнения (1) в общем случае. Существует лишь свойства решения.

Для любого фиксированного справедливы 3 теоремы:

1. Справедливо одно и только одно из следующих 2 утверждений:

а) однородное уравнение (1) имеет ненулевые решения.

б) соответствующее неоднородное уравнение (1) имеет единственное решение

при любой правой части.

2) Однородное уравнение (1) и союзное однородное уравнение (1) имеют конечное и при том одинаковое число решений.

3) Если реализуется первое условие теоремы (1), то для разрешимости неоднородного уравнения (1) чтобы

Определение: собственными значениями однородного уравнения (1) называются

значения параметра , при котором это уравнение имеет ненулевые

решения.

Определение: Спектром однородного уравнения (1) называется совокупность его

собственных значений.

Теорема 4: любой конечный интервал действительной оси содержит разве что конечное число точек спектра.

Эти теоремы называются теоремами Фредгольма.

Определение: Ядро уравнения (1) называется вырожденным, если оно имеет вид

Функции и является лин. незав.

Подставим в уравнение (1) вырожденное ядро:

(3)

Обозначим k=1,…,n

Уравнение (3): (4)

Из уравнения (3) (3^’)

Умножим правую и левую части уравнения (3) на b_j(x), j=1,…,n и интегрировать

(5) j=1,…,n

(6) j,k=1,…,n

j=1… n

(7) j=1,…,n

- система линейных алгебраических уравнений

Для того чтобы решить уравнение (1) в случае вырожденного ядра необходимо по формулам (6) и (7) найти константы и , составить систему (8) и записать по формуле (4) решение исходного уравнения.