Линейные системы.
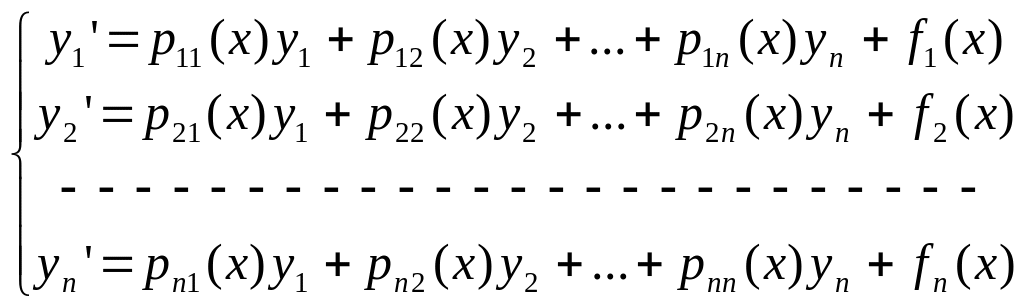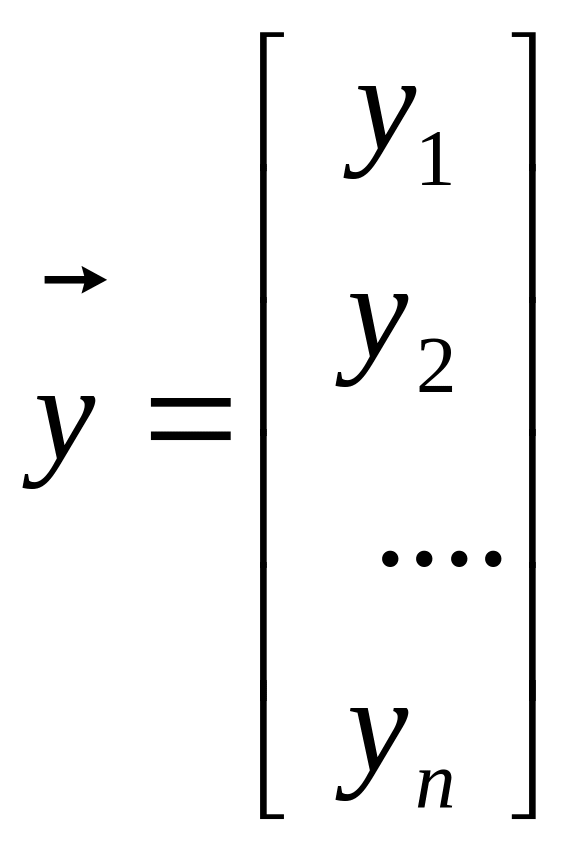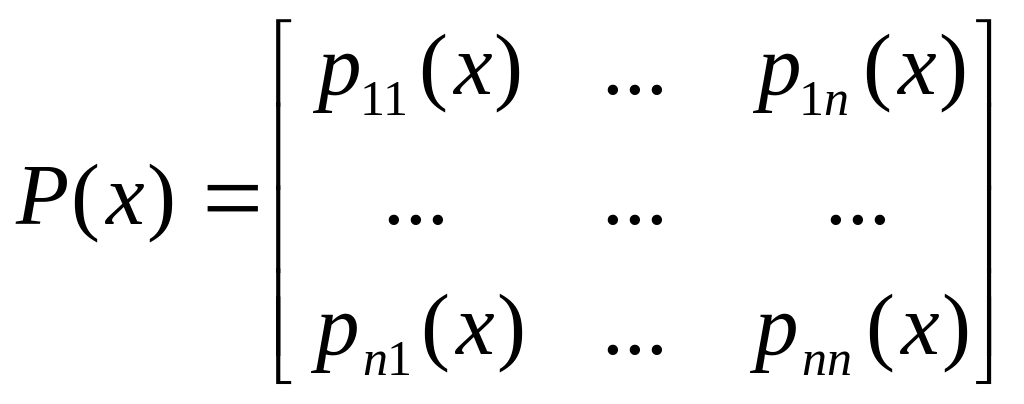
(1)
?
,
;
;
(1’)
Если
то (1) называется однородной системой,
иначе называется неоднородной.
1.однородные системы
(2)
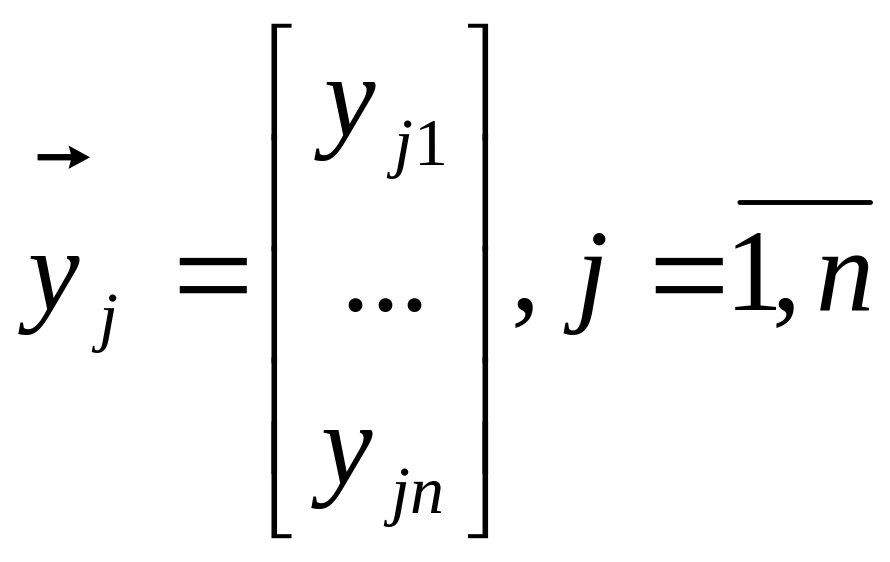(3)
Опр: Векторы (3) наз. лин. Зависимыми
если существуют такие
не все равные нулю, что
. Если это равенство справедливо лишь
при
,
то векторы называются лин. не зависимыми.
Опр: фундаментальной системой решений системы (2) наз. совокупность n лин. нез. вект. является ее решениями
Опр: определителем Вронского или вронскианом (3) наз. определитель
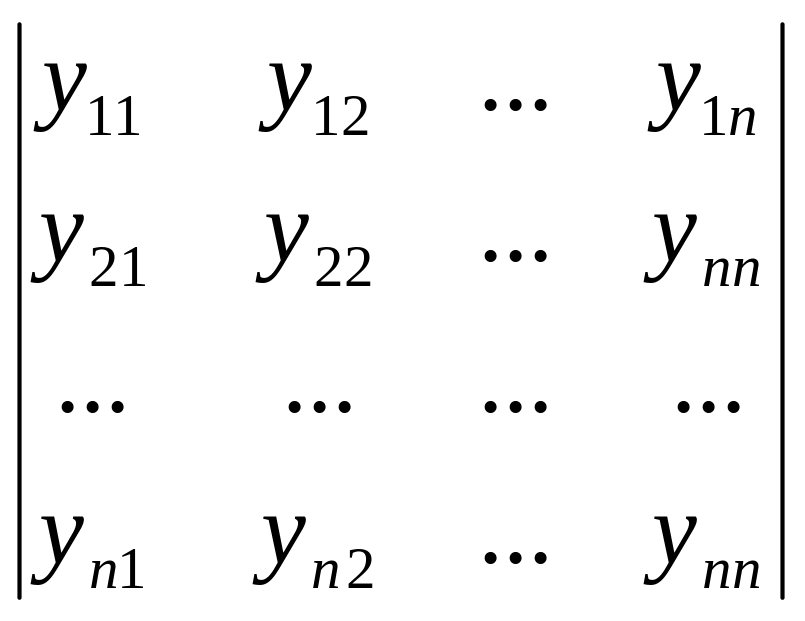обозначение Δ,Δ(x),
Теор1: пусть векторы (3) лин. зав. на I тогда Δ(x)≡0
Теор2: пусть векторы (3) реш. сист. (2) тогда справедливо одно и только одно утв.
А)Δ(x)≡0 (равносильно (3) л.з.)
B)
(3)
лин. независимо)
Теор3: общее решение (2) имеет вид,
где
постоянные произведения, действительных
- ФСР (2)
2. линейные однородные системы с постоянными коофициентами
(Случай n=3)
,
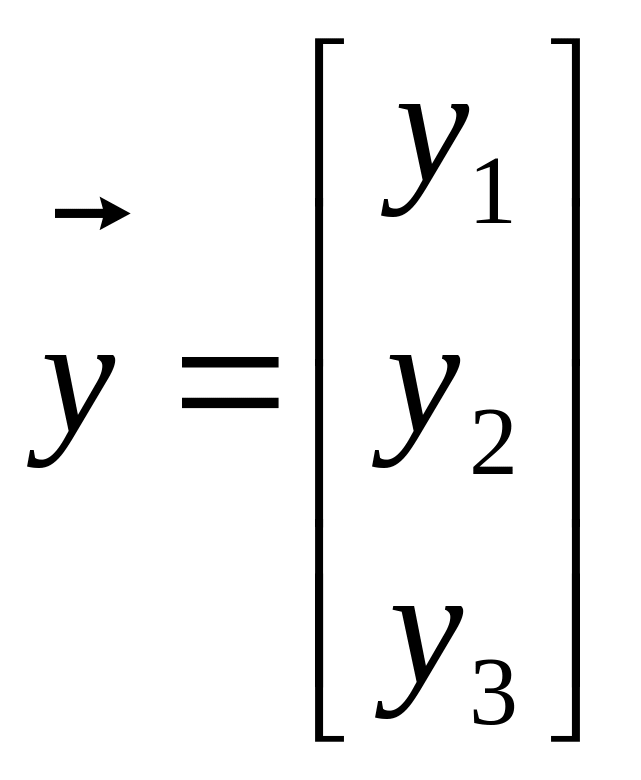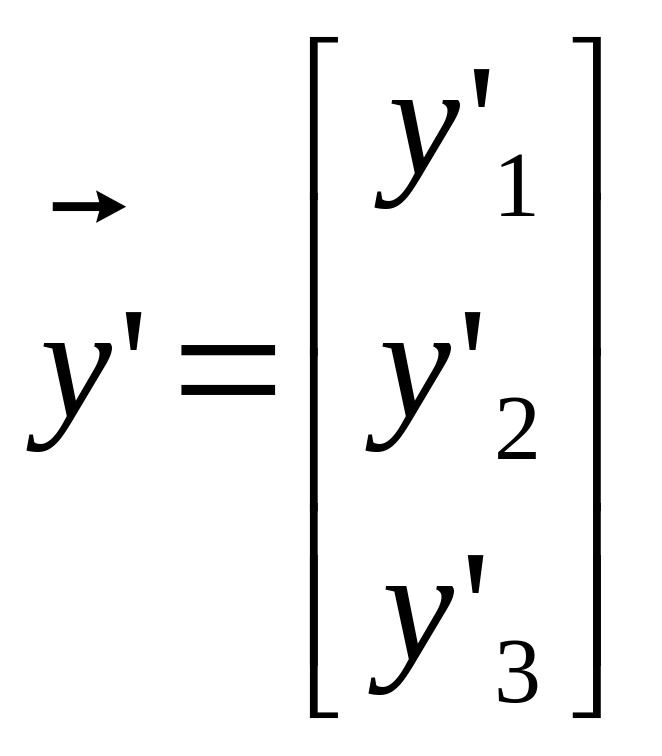, A=
(4) 
k,j=1…3
j=1,…,3ф.с.р. системы (4)
Предположим что А имеет действительные
собственные значения
линейно независимые векторы обладающие одним из следующих св-в.
1) собственные векторы А
, j=1,2,3
собственное значение соответствующего
собственного вектору
2)
собственный вектор А
присоединенный вектор к
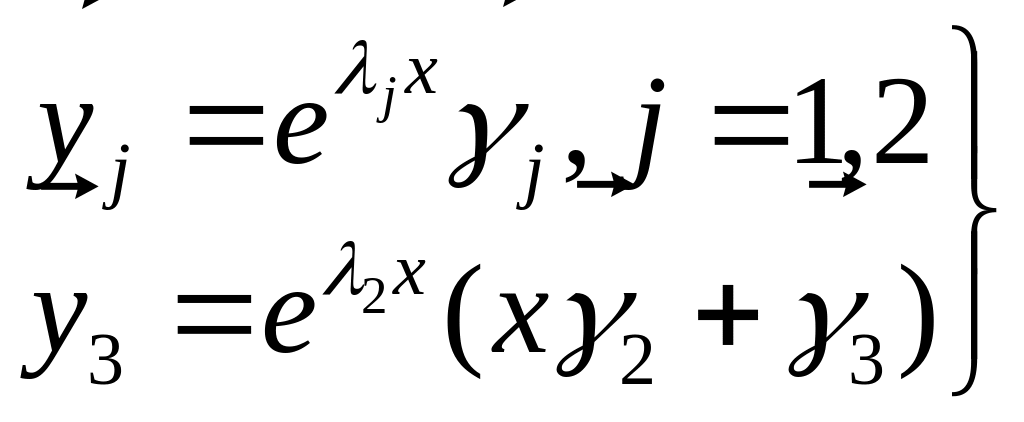(5)
где
собственные значения для векторов
3)
собственный вектор А
присоединенные векторы к
λ собственное значения для вектора
Для А
(
>0)
собственное значение
собственного вектора с
какой либо собственный вектор с
Доказательство формулы (5):
Δ(x) , Δ(0) следовательно
Δ(0) определитель, столбцы
которого
По (Т2) векторы (5) линейно независимы
j =1,2
определение
собственное значение собственного
вектора
по
опр. соб. вектора.
истинно по опр. соб. вектора.
3.линейная неоднородная система
Предположим (3) ф.с.р.
составить и
1) решить ф.с.р.
2
3)
n=2 лучше методом исключений
Устойчивость решений.
решение
О
пр.
Решение
системы (1) называется устойчивым (в
смысле Ляпунова) если
такое что для всякого решения
для которого выполняется неравенство
выполнялось также неравенство
где
расстояние
в n-мерном
пространстве.
Опр.
Решение
системы (1) называется устойчивым
асимптотическим, если оно устойчиво и
кроме того
такое что
Считаем сначала что система (1) имеет нулевое решение, и далее будем говорить об устойчивости или неустойчивости нулевого решения.
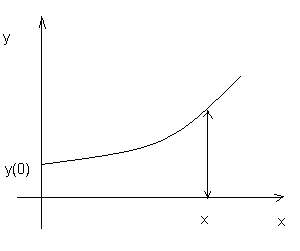
Значит
нулевое решение неустойчиво
н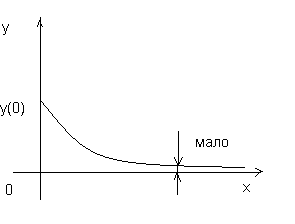
улевое
решение устойчиво асимптотически
Допустим
функции
Опр. Системой первого приближения для системы (1) называется система:
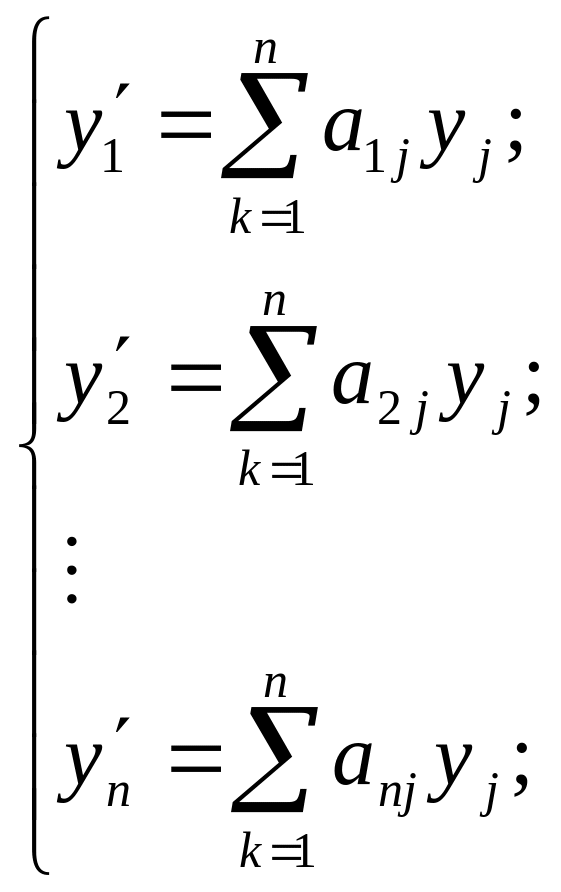(2) 
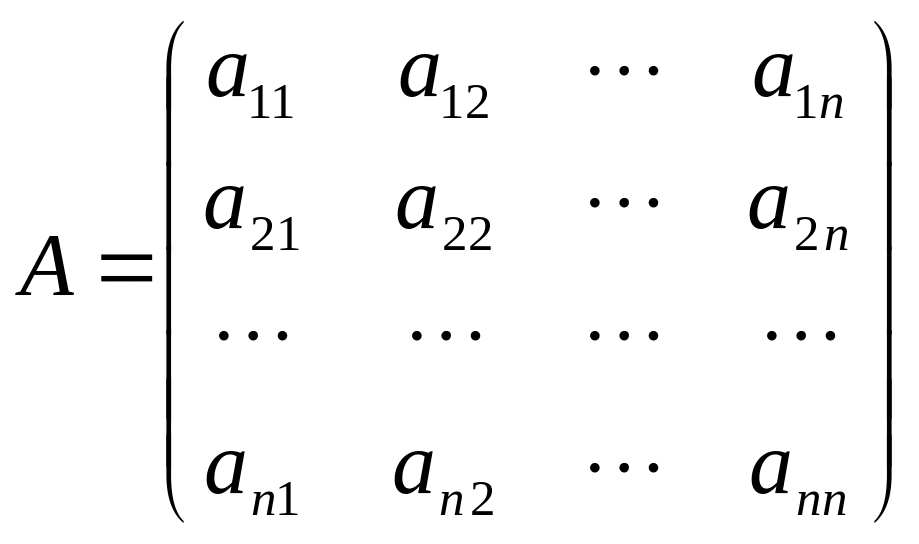
Теорема: Если все собственные значения матрицы А отрицательную действительную часть, то нулевое решение асимптотически устойчиво, а если хоть одно значение матр. А имеет положительную часть то решение неустойчиво.
Опр.
Матрицей Гурвица многочлена
(3) называется следующая матрица:
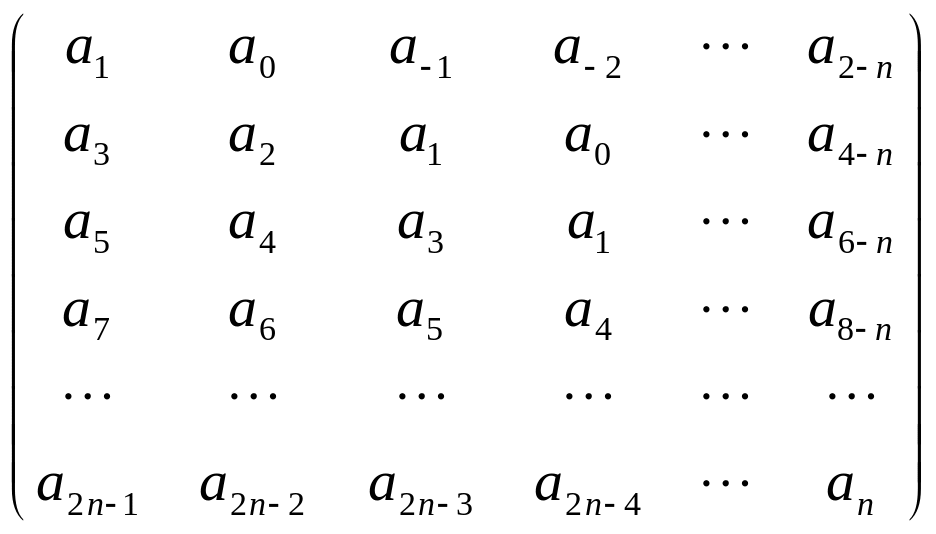
-где
-коэффициенты (3) для k=1,2,…,n
при
k<0
и k>n
Критерий Рауса-Гурвица
Для того чтобы корни многочлена (3) имели отрицательную действительную часть, необходимо и достаточно чтобы были положительными все главные миноры соответствующей матрицы Гурвицы.