Линейные, неоднородные уравнения высшего порядка.
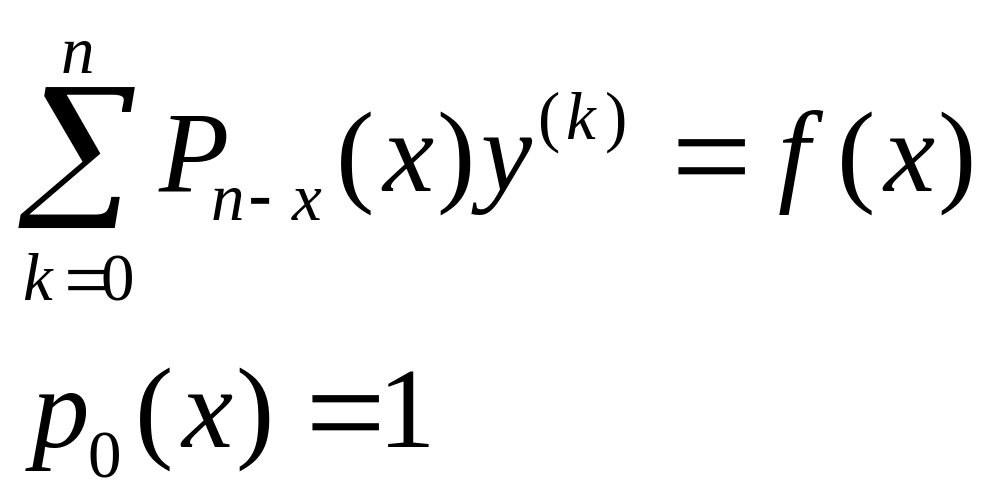
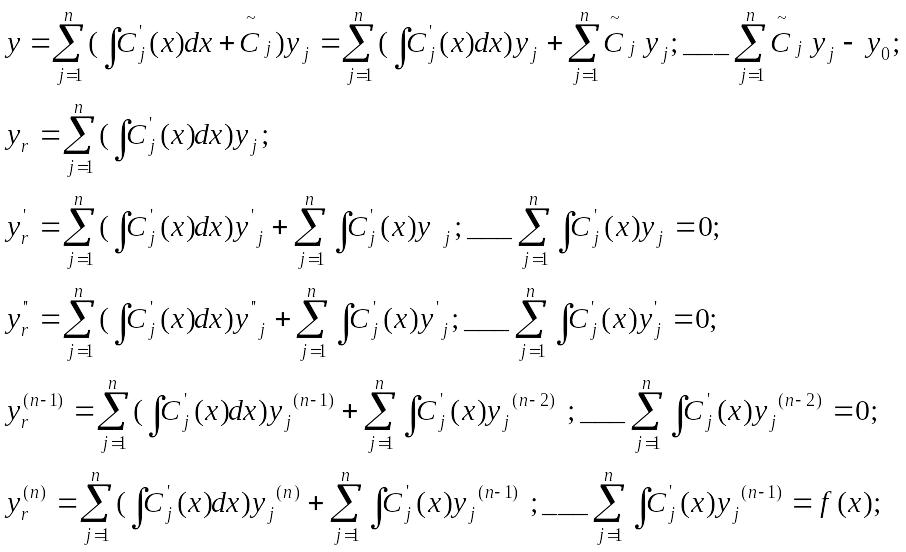
Свойства уравнения (1):
3) Разность двух любых решений неодн.= решению однородного.
4)
Метод Лагранжа (метод вариаций производных постоянных)
1) Составить и решить систему алгебраических уравнений
Доказательство:
Для
(и еще +f(x) для k=n )
Метод неопределенных коэффициентов.
(Для уравнений с постоянными коэффициентами)
1)
-квазимногочлен
k=0,
,
если
не является корнем соответствующего
уравнения а если
,
то
берется кратности этого корня.
берется неопределенное, а затем находится
подстановкой в
.
2)
Формула Остроградского-Лавуазеля
(1)
Теорема 1: Пусть у1,y2,…,yn- л. Незав.
Уравнение вида (1). Для каждого этажа
функция является фундаментальной
системой решения .
Док-во:
1)
Существование: 
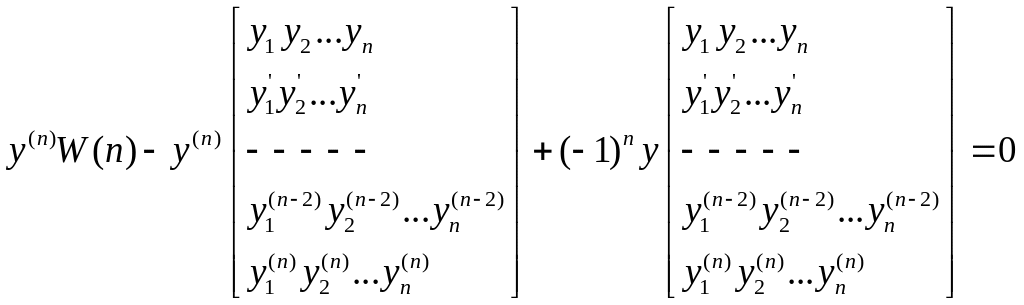(2)
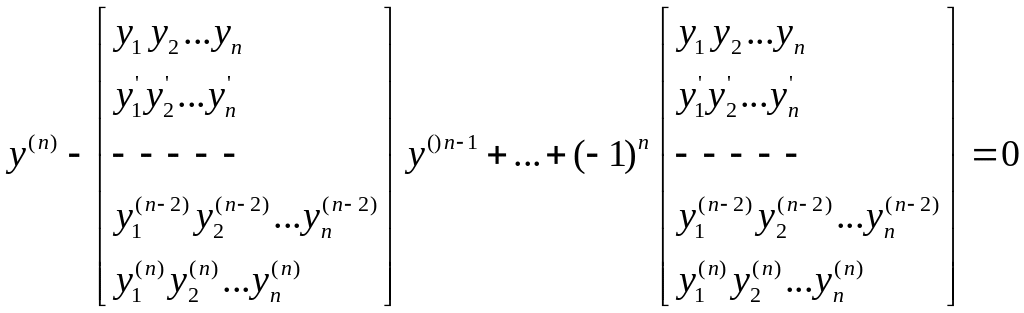(3)
2) Единственность:
(4)
-непр-на.
Если функция неправильна в некоторой точке то она неправильна в некоторой окрестности этой точки.
реш.
(1)и (4), то тогда это реш. Разности (1) и
(4)
Исходное уравнение не может иметь решений больше чем его порядок.
Теорема 2:
Ф.С.Р.
уравнения (1), W(x)
фикс.
спарв. Формула
(ф.О.-Л.)
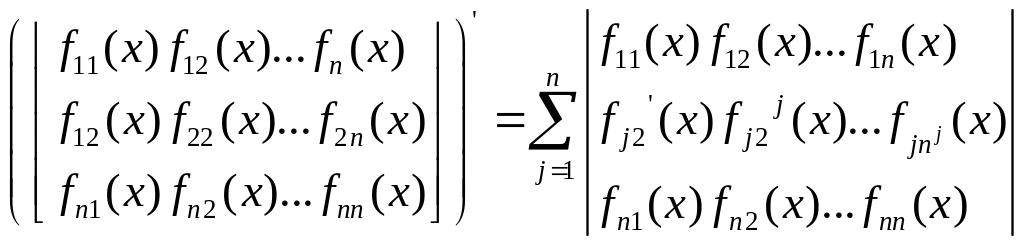
По формуле Ф.С.Р. мин. Одн. Уравнения восстан ед. образом. (2), (3) восстан. По Ф.С.Р.
;
;
;
;
; 
;
Линейные уравнения Эйлера
(1)
(2)
(2’)
Определение: Определяющим уравнением
для (2) называется уравнение
(3)
Правило нахождения Ф.С.Р. уравнения (2)
Вначале найдите корни соответствующего определенного уравнения (3) в соответствии с их кратностью.
Каждому действ. , кратн. k соответствующий функции
а компл.
кратн. S
Функцию указанным образом сопоставляют всем действительным корням и комплексным числам.
Линейные однородные уравнения (производного порядка).
(1)
- ?
- коэффициенты уравнения непрерывны на
.
(1’)
(1”)
- оператор (линейный)
Свойство 1: Линейная комбинация с коэффициентами решения (1) сама будет решением (1).
Свойство 2:
на
решение уравнения (1) такое, что
.
Теорема 1:
- решение (1)
л.з.
Доказательство:
- ?
- не нулевые решения системы.
- решение (1)
В силу соотв.
Теорема 2: Пусть - решения уравнения (1), тогда справедливо одно и только одно из следующих двух утверждений:
1)
(
л.з.)
2)
(
л.незав.)
Доказательство:
тогда по Т. 1 решение л.з.
Определение: Фундаментальной системой решений уравнения (1) называется n его независимых решений.
Теорема 3: уравнения (1) фундаментальная система решений.
Доказательство: фиксируем
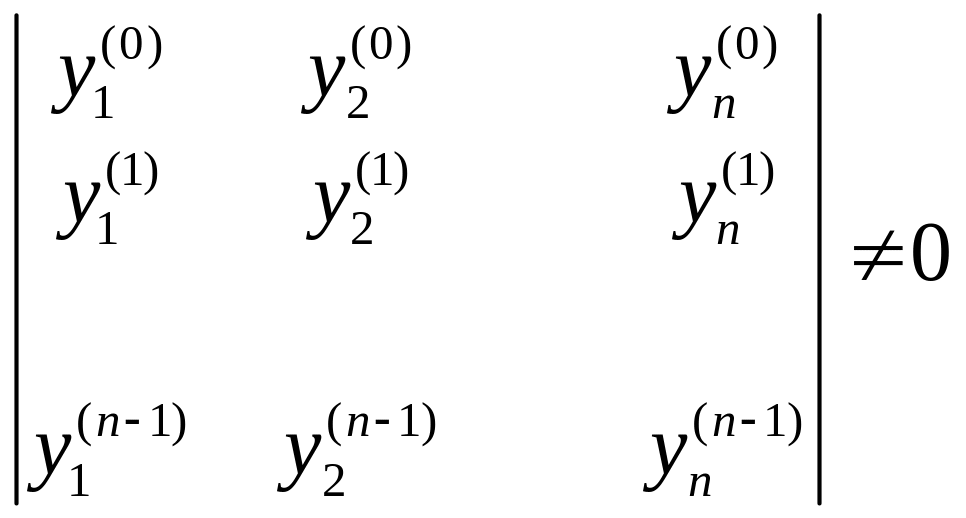
Теорема 4:
- ф.с.р.
Доказательство:
Фиксируем
- ?
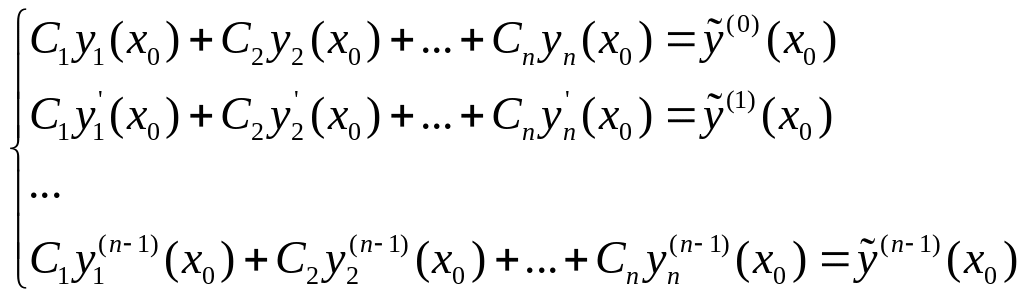
Следствие: (1), n
Доказательство:
- л.незав.
ф.с.р.
