Лекции по дифференциальным уравнениям.
Факультет радиофизики и электроники Преподаватель: Шилин а.П.
Введение.
Опр. ОДУ порядка n, где
n _N, называется
уравнение вида
-
(1)
х – независимая переменная.
у – зависимая переменная.
у=у(х) – искомая функция.
y', y′′,
…,
-
gпроизводные искомой
функции.
F – заданная функция.
Порядок уравнения – порядок старшей производной, которая присутствует в уравнении.
Интегрирование – решение уравнения.
График любого решения ДУ – интегральная
кривая
- уравнение, разрешенное относительно
старшей производной.
у'=f(x,y) – (2) – уравнение первого порядка разрешённое относительно производной.
Решение ДУ называе6тся полученным в квадратурах, если оно выражено через элементарные функции посредствам арифметических операций, операции образования сложенной функции и операции нахождения интеграла. При этом решение может быть функцией, заданной явной, неявной, параметрической, а неопределенные интегралы могут быть не берущимися.
Начальным условием для (2) называется следующее дополнительное условие у(х0)=у0 – (3), (х0,у0) – точка из f(x,y).
(2), (3) – задача Коши.
Важнейшие случаи уравнения 1-го порядка, разрешенного относительно производной.
(1)
– нормальная форма
(1’)
(1”)
(1(4))
– дифференциальная форма.
1. Уравнение с разделенными переменными:
2. Уравнение с разделяющимися переменными:
проверить эти случаи после интегрирования
g(y)=0 - ?
3. Уравнение вида:
у=у(х) - ?
z=z(x) - ?
z=ax+bx=ax+by(x)
4. Однородное уравнение:
(
- ?)
5. Уравнение вида:
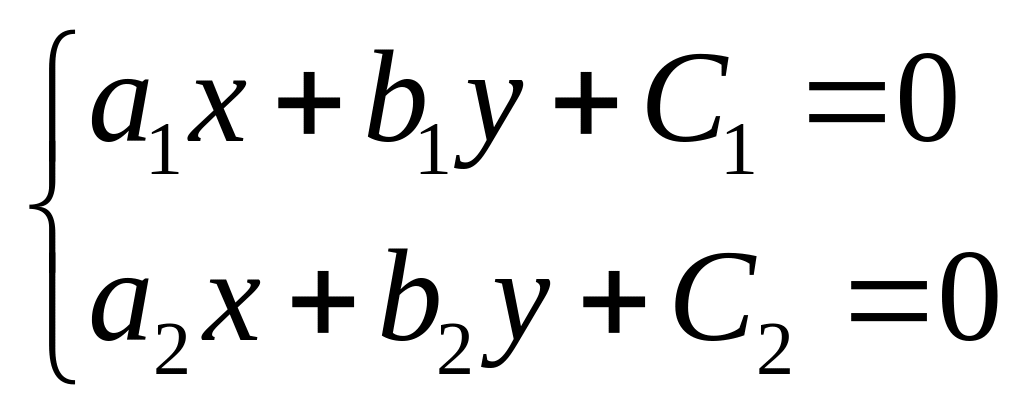
- решение системы
,
-?
6. Уравнение в полных дифференциалах.
Определение: Уравнение
– (1) называется уравнением в полных
дифференциалах, если
такая, что
.
- решение уравнения
,
- непрерывно дифференцируемы.
(1) рассмотрим в односвязной области либо совокупности областей.
Определение:
называется интегрирующим множителем
для функции (1), если после умножения на
эту функцию, уравнение становится
уравнением в полных дифференциалах.
7. Линейные уравнения:
- ?
- коэффициент заданы
- свободный член
- линейный оператор
при
- уравнение однородно
при
- не однородно.
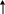
конкретная первообразная
1). Метод Лагранжа (метод вариаций произвольной постоянной):
2). Метод неоднородных коэффициентов:
а)
квазимногочлен (α=0 - многочлен
где
- ?
при
б)
- ?
8. Уравнение Бернулли:
(
?)
(
- ?)
9. Уравнение Риккати:
- частное решение
(
- ?)
- ?
Уравнения 1-го порядка, не разрешенные относительно производной.
(1)
1)
(неполное уравнение, разрешенное
относительно х)
- параметр
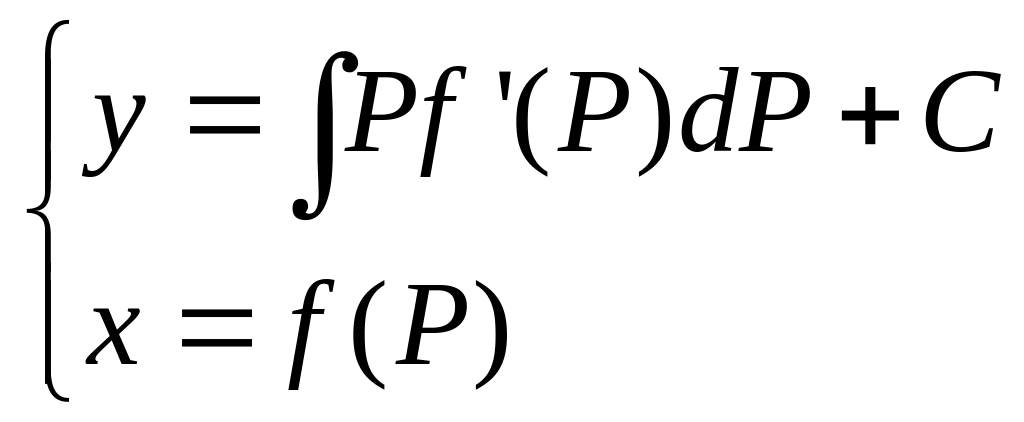
2)
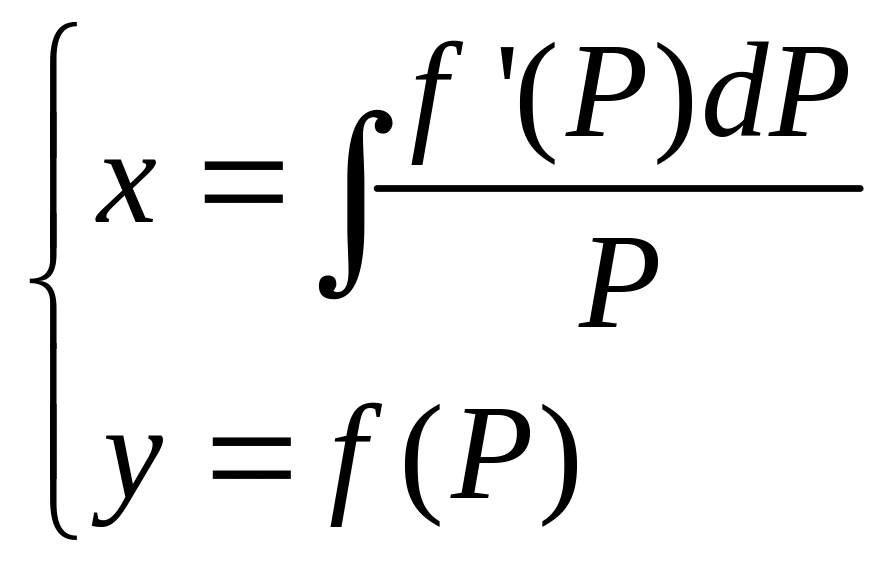
3)
- ?
4)
(2)
- ?
Частный случай (2):
а)
- уравнение Клеро
- общее решение уравнения Клеро
особое решение уравнения Клеро
б)
- уравнение Лагранжа
|:
- ?
Уравнения высших порядков:
(1)
(2)
- начальные условия
(1), (2) – задача Коши
Теорема: Пусть
является непрерывными функциями
.
Тогда в точке
решение задачи Коши (1), (2).
(2)
1)
…
n
2)
…
3)
(3)
(
-?)
…
4)
(
-?)
5) частный случай уравнения (3)
т
свойство, однородности степени
относительно переменной
.
(
-?)
…
Подставим в (3)
6) в уравнении (3) левую часть можно записать:
- (3) – уравнение точных производных.
в общем случае нельзя найти функцию Ф.
Приложения дифференциальных уравнений (задача о форме отражающей поверхности):
Определить форму зеркала, которое собирает лучи в одну точку.
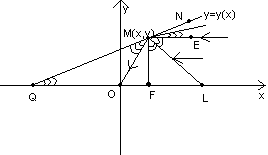
MQ- касательная;
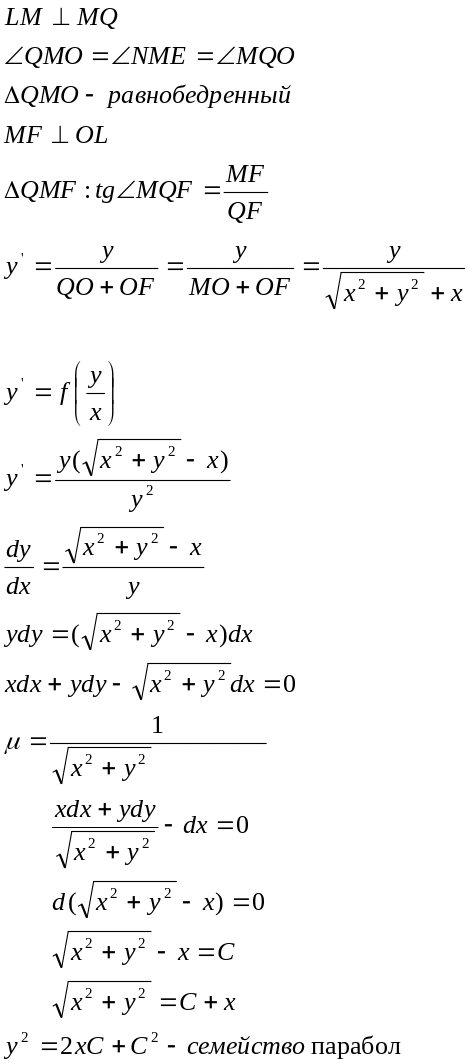
Система дифференциальных уравнений.
(1)
-? 
(2)
– начальные условия
(1), (2) – задачи Коши
Теорема: в некоторой окрестности
является непрерывной.
в некоторой окрестности
- решение единственное (1), (2).
связь между (1) и
-
(3)
уравнения (3) можно заменить на (1).
…
От (1) к (3) не всегда можно сделать
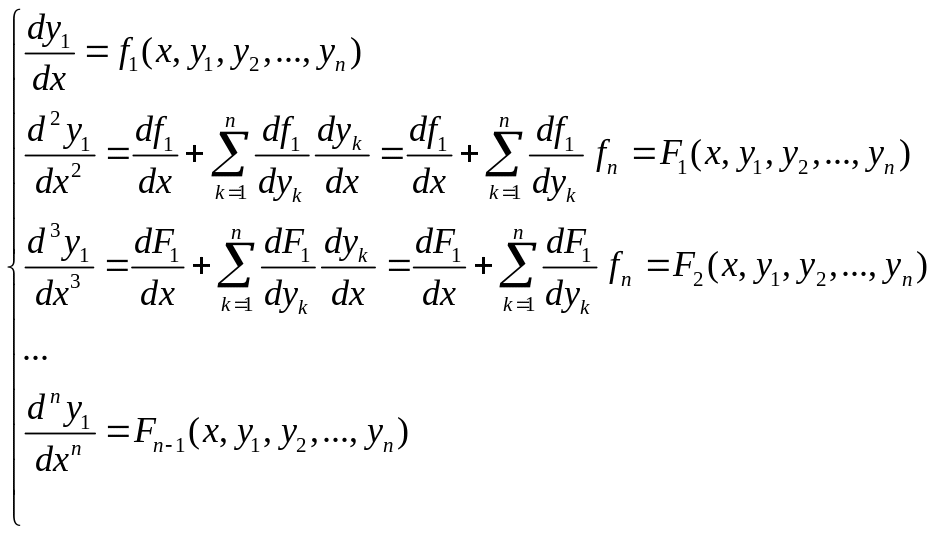
будем исключать
останется соотношение с
- метод исключения.
Определение. непрерывный дифференциал
называется интегралом системы (1), если
её дифференциальное вычисление в силу
этой системы соответственно равно нулю.
Определение. Первым интегралом
системы (1) называется соотношение
,
,
-
интеграл.
Общий интеграл (1) – совокупность и её первых интегралов, для которых соответственно интегралы не зависимы.
…
Система (1) считается решенной, если найден её общий интеграл.
(1) – называется системой в нормальной форме.
Также можно записать в симметрической форме:
- (4)
Для перехода к (1) приравниваем всё к последнему:
Для нахождения общего интеграла проще решать систему в симметричной форме и использовать свойство равных дробей:
Уравнения в частных производных первого порядка.
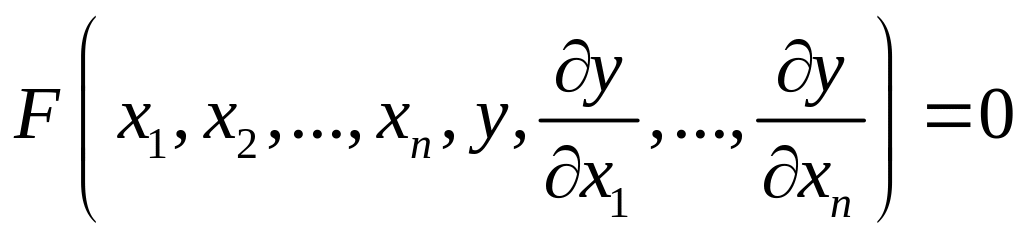(1)
- ?