2.1.3 Корректировка основного варианта

Корректировка основного варианта необходима, чтобы учесть тип ригеля и величину опирания конструкций на стены.

Величину опирания плит на стены принимаем равной 120 мм, ригелей на стены –380 мм. Приведем эскиз проектируемого основного варианта проектируемого перекрытия с необходимыми разрезами (Рисунок 2.1.3.1).

Рисунок 2.1.3.1 – Выбранный вариант с необходимыми размерами

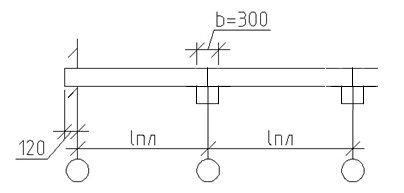
Рисунок 2.1.3.2 – Разрез 1-1

Определяем пролет плиты:

; (2.1.3.1)

м.

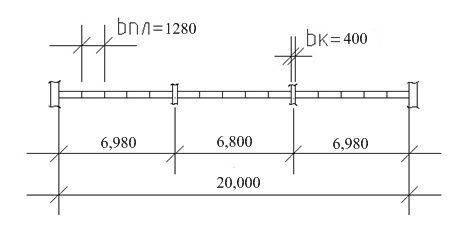
Рисунок 1.3.3 – Разрез 2-2

Определяем пролет крайнего ригеля:

; (2.1.3.2)

м.

Определяем пролет среднего ригеля:

; (2.1.3.3)

м.

2.2 Расчет и конструирование плиты перекрытия

2.2.1 Назначение размеров плиты перекрытия, сбор нагрузок на плиту перекрытия

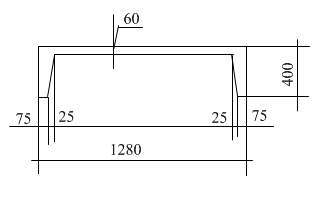
Рисунок 2.2.1.1 – Схема ребристой плиты

Производим сбор нагрузок на квадратный метр панели перекрытия.

Нагрузка от собственного веса панели определяется по следующей формуле:

; (2.2.1.1)

где - площадь сечения бетона:

- плотность бетона,

- ширина плиты.

Таблица 2.2.1.1 – Нагрузки на 1 м² плиты

Нагрузка	Норм. Значение	Коэффициент надежности	Расчетное значение
Постоянная нагрузка
1. Собственный вес плиты	2,66	1,1	2,93
2. ЦПС	0,36	1,3	0,47
3. Керам. Плитка	0,144	1,2	0,17
ИТОГО	3,16		3,57
Временная нагрузка
Полезная	=10	1,2	12
			15,57
Кратковременная	1,5	-	1,8
Длительная	8,5	-	10,2

2.2.2 Определение усилий от нормативных и расчетных нагрузок

Сборная плита рассчитывается как шарнирно опертая балка на двух опорах.

Расчетные пролеты определяем между серединами площадок опирания. Принимаем их равными 120 мм. Тогда:

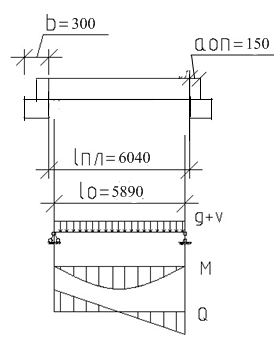
Рисунок 2.2.2.1 – Расчетная схема с назначением размеров и характером эпюр внутренних усилий

; (2.2.2.1)

м;

; (2.2.2.2)

м;

1. Определяем усилия для расчетов по первой группе предельных состояний (расчеты на прочность).

; (2.2.2.3)

;

; (2.2.2.4)

;

2. Определяем усилия для расчетов по второй группе предельных состояний.

а) Усилия от действия полных нагрузок:

; (2.2.2.5)

;

; (2.2.2.6)

;

б) Усилия от действия длительных нагрузок:

; (2.2.2.7)

;

; (2.2.2.8)

;

2.2.3 ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ

Характеристики материалов определяются согласно заданию на проектирование, а также в соответствии с СП 52-101-2003 «Бетонные и железобетонные конструкции без предварительного напряжения арматуры». (Таблица 2.2.3.1).

Таблица 2.2.3.1 – Характеристики материалов

Материал
Бетон	Продольная арматура	Поперечная арматура
Класс B20	Класс А500	Класс B500, А240, А400
; ; ; ; ; ; .	; ; ;	; ; .

2.2.4 ПРОВЕРКА РАЗМЕРОВ СЕЧЕНИЯ ПЛИТЫ ПЕРЕКРЫТИЯ

Проверку размеров сечения плиты произведем, исходя из расчета на прочность по наклонным сечениям самой тонкой части сечения. Проверим соблюдение условия:

.

кН.

, (2.2.4.1)

где b – суммарная толщина всех ребер плиты, b = 0,150 м;

– рабочая высота сечения плиты.

, (2.2.4.2)

где h – высота плиты, h = 0,40 м;

d – диаметр продольной арматуры, предварительно принимаем d = 32 мм;

- величина защитного слоя бетона, согласно п.8.3.2 СП 52-101-2003 принимаем = 32 мм.

м.

Тогда

0,3 10,35 = 163,94 кН

58,69<163,94 кН.

Условие выполняется. Окончательно принимаем размеры плиты.

2.2.5 РАСЧЕТ ПЛИТЫ ПЕРЕКРЫТИЯ ПО I ГРУППЕ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ

К расчету принимаются усилия, возникающие от расчетных нагрузок

2.2.5.1 РАСЧЕТЫ ПО СЕЧЕНИЯМ НОРМАЛЬНЫМ К ПРОДОЛЬНОЙ ОСИ

Для дальнейшего расчета необходимо привести сечение, нормальное к продольной оси элемента, к тавровому (Рисунок 2.2.5.1), поскольку плита работает как однопролетная шарнирная балка, следовательно, сжатая зона всегда будет располагаться в верхней части сечения.

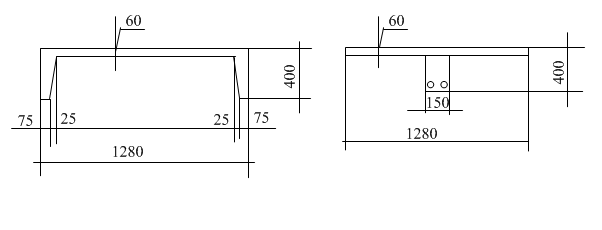
Рисунок 2.2.5.1.1 – Исходное и тавровое сечения

Проверим, выходит ли сжатая зона за пределы полки под действием максимального момента . Для этого определим, какой изгибающий момент воспринимается сечением при высоте сжатой зоны равной ширине полки:

, (2.2.5.1.1)

где - высота полки, ;

– ширина полки, = 1280 мм;

кН м;

Получили, что

,

следовательно к расчету можно принять прямоугольное сечение 1,280х0,4 м² с рабочей высотой .

Для определения требуемой площади арматуры определим вспомогательный коэффициент для максимального значения изгибающего момента по формуле (1.3.5.2.2):

;

.

Для вспомогательный коэффициент и относительную высоту сжатой зоны бетона .

Определим значение граничной высоты сжатой зоны бетона для нашего сечения по формуле (1.2.5.2):

;

.

Условие выполняется, значит, изменение размеров сечения не требуется.

Определим требуемую площадь поперечного сечения продольной арматуры для каждого значения изгибающего момента по формуле (1.2.5.3):

;

;

Принимаем 2 стержня диаметром 20 мм. Армирование покажем на рисунке 2.2.5.1.2.

Рисунок 2.2.5.1.2 – Продольное армирование плиты

Выполним проверку прочности с подобранной арматурой. Для этого определим фактическую высоту сжатой зоны по формуле (1.3.5.2.3):

,

где - фактическая площадь арматуры, ;

;

Полученное значении высоты сжатой зоны меньше ширины полки. Прочность обеспечена.

Вычислим момент, который может воспринимать сечение по формуле (1.3.5.2.4):

;

кН м;

> М_max

95,01>86,42.

Проверка прочности выполнена, прочность обеспечена.

2.2.5.2 РАСЧЕТЫ ПО СЕЧЕНИЯМ НАКЛОННЫМ К ПРОДОЛЬНОЙ ОСИ

Для расчета на прочность сечений, наклонных к продольной оси выделяем пролетные и приопорные участки (Рисунок 2.2.5.2.1).

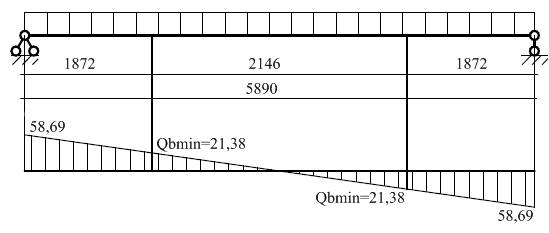
Рисунок 2.2.5.2.1 – К расчету по наклонным сечениям

При расчете по прочности сечений, наклонных к продольной оси элемента, необходимо соблюдения следующих условий:

1) ;

2) ;

3) ,

где Q - максимальная поперечная сила на рассматриваемом участке, кН;

- прочность по бетонной полосе между наклонными сечениями, кН;

- прочность по наклонному сечению, кН;

- прочность бетона между хомутами, кН.

Первое условие было проверено нами в п.1.3.4, и будет соблюдаться для всех участков всех пролетов.

В условии 2:

,

где - поперечная сила, воспринимаемая бетоном в наклонном сечении, кН;

- поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении, кН;

Для поперечного армирования необходимо выполнение условия (1.3.6.1):

,

где – диаметр поперечных стержней каркаса;

– диаметр продольных стержней (принимаем 28 мм из-за расчета по трещиностойкости)

.

Принимаем класс .

П ри расчете пролетных участков будем полагать, что поперечная сила воспринимается только бетоном, а поперечную арматуру будем устанавливать конструктивно согласно требований:

→ ;

;

принимается кратным 50 мм в сторону уменьшения.

.

;

; (2.2.5.2.1)

где - суммарная ширина ребер плиты, м.

кН;

Кроме того необходимо, чтобы выполнялось и условие 3. Таким образом принятый шаг поперечной арматуры не должен превышать допускаемый:

;

; (2.2.5.2.2)

.

250мм < 704 мм – условие выполняется.

Длину пролетного участка определим графически (Рисунок 2.2.5.2.1).

При расчете приопорных участков поперечная арматура будет учитываться в расчете:

;

Также для поперечной арматуры необходимо соблюсти следующие конструктивные требования:

→ ;

;

, (2.2.5.2.3)

где - максимальная поперечная сила на участке, кН.

,

Выбираем наименьшее значение кратно 50 мм.

.

Произведем проверку прочности приопорного участка с принятым армированием. Для этого определяем интенсивность хомутов по формуле (1.3.6.5):

,

где n – количество каркасов (n=2);

.

Для учета поперечной арматуры в расчете проверяем выполнение условия (1.3.6.6):

.

.

114,0 > 30,4 – условие выполняется, значит учитываем поперечную арматуру.

Находим длину проекции опасного сечения (1.3.6.7):

,

где – условный момент, который найдем по формуле (1.3.6.8):

;

кН·м;

.

Должно выполняться условие:

,

,

Поперечную силу, воспринимаемую бетоном в наклонном сечении найдем по формуле (1.3.6.9):

;

кН;

Поперечную силу, воспринимаемую поперечной арматурой в наклонном сечении найдем по формуле (1.3.6.10):

;

;

Прочность по наклонному сечению находится по формуле (1.3.6.11):

;

кН.

кН.

Условие выполняется.

2.2.6 РАСЧЕТЫ ПЛИТЫ ПЕРЕКРЫТИЯ ПО II ГРУППЕ ПРЕДЕЛЬНЫХ СОСТОЯНИЙ

К расчету принимаются усилия, возникающие от нормативных нагрузок. В расчетах следует учитывать работу бетона в растянутой зоне. Первым выполняем расчет по образованию трещин, поскольку от наличия или отсутствия трещин зависит ход расчета по деформациям.

2.2.6.1 РАСЧЕТЫ ТРЕЩИНОСТОЙКОСТИ СЕЧЕНИЙ, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ

Условие по раскрытию трещин при диаметрах 20, 22, 25 мм не прошло, поэтому принимаем 2 стержня диаметром 28 мм с общей площадью 1232 мм².

Выполняем расчет на образование трещин. Трещины не образуются, если соблюдается следующее условие:

, (2.2.6.1.1)

где – максимальный изгибающий момент от полных нормативных нагрузок;

– момент, который воспринимает сечение перед образованием трещин.

, (2.2.6.1.2)

где - упругопластический момент сопротивления приведенного сечения.

, (2.2.6.1.3)

где - момент сопротивления приведенного сечения;

- коэффициент, учитывающий упруго-пластичную работу бетона; определяется по таблице 4.1 Пособия по проектированию бетонных и железобетонных конструкций без предварительного напряжения арматуры.

Для определения коэффициента приводим сечение плиты к тавровому (ребристые плиты) (Рисунок 2.2.6.1.1).

Рисунок 2.2.6.1.1 – Схема приведения сечения плит к эквивалентному тавровому сечению

Для дальнейшего расчета необходимо ввести понятие приведенного сечения – сечения, выполняемого путем приведения арматуры к эквивалентной площади бетона, рассчитываемой по формуле:

, (2.2.6.1.4)

где - коэффициент, рассчитываемый по формуле:

; (2.2.6.1.5)

;

м².

Тогда площадь одного стержня:

; (2.2.6.1.6)

где - количество продольных арматурных стержней в плите;

м².

Изобразим приведенное сечение на рисунке 2.2.6.1.2.

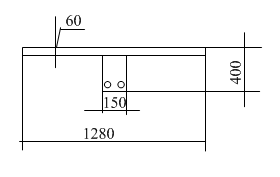
Рисунок 2.2.6.1.2 – Приведенное сечение

Вычислим характеристики приведенного сечения.

Площадь приведенного сечения:

, (2.2.6.1.7)

где - площадь исходного сечения;

м² =1365 см².

Центр тяжести у приведенного сечения смещается вниз по сравнению с эквивалентным. Положение центра тяжести приведенного сечения найдем по формуле:

, (2.2.6.1.8)

где - статический момент площади приведенного сечения, см³.

Статический момент найдем относительно нижней грани по формуле:

, (2.2.6.1.9)

где - отдельно взятая площадь бетонного сечения, см²;

- расстояние от отдельно взятой площади бетонного сечения до нижней грани (Рисунок 2.2.6.1.3), см;

Рисунок 2.2.6.1.3 – К расчету статического момента

; (2.2.6.1.10)

где - расстояние от нижней грани до центра тяжести арматуры;

м³= 37516 см³;

см.

Определим момент инерции приведенного сечения относительно оси, проходящей через его центр тяжести.

; (2.2.6.1.11)

где - момент инерции отдельно взятой части бетонного сечения относительно оси, проходящей через ее центр тяжести, см⁴,

; (2.2.6.1.12)

см⁴;

см⁴;

; (2.2.6.1.13)

см⁴;

см⁴;

см⁴;

см⁴.

Определим момент сопротивления приведенного сечения относительно нижней растянутой грани по формуле:

; (2.2.6.1.14)

см³;

см³;

кН м.

,

– условие не выполняется, следовательно, необходимо произвести расчет на раскрытие трещин.

Ширина раскрытия трещин, согласно СП 52-101-2003, не должна превышать

следующих значений:

- при продолжительном раскрытии трещин ;

- при непродолжительном раскрытии трещин .

Полная ширина раскрытия трещин определяется как

, (2.2.6.1.15)

где - ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок;

- ширина раскрытия трещин от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок;

- ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок.

Продолжительная ширина раскрытия трещин:

.

Далее выполняем расчет , , от соответствующих усилий, найденных в п.2.2.2, находим величины продолжительного и непродолжительного раскрытия трещин и сравниваем их с допускаемыми. В случае, если вычисленные значения ширины раскрытия трещин превышают допускаемые, увеличиваем диаметр продольной арматуры.

Фактическая ширина раскрытия трещин определяется по формуле:

, (2.2.6.1.16)

где - напряжение в продольной арматуре в сечении с трещиной от соответствующей внешней нагрузки;

- расстояние между смежными трещинами;

- коэффициент, учитывающий неравномерное распределение деформаций растянутой арматуры между трещинами;

- коэффициент, учитывающий продолжительность действия нагрузки; при непродолжительном действии нагрузки, при продолжительном;

- коэффициент, учитывающий профиль продольной арматуры, для арматуры периодического профиля;

- коэффициент, учитывающий характер нагружения, для изгибаемых элементов .

, (2.2.6.1.17)

где - изгибающий момент от соответствующей нагрузки;

- расстояние от центра тяжести растянутой арматуры до центра тяжести сжатой зоны бетона, ;

- площадь продольной арматуры.

;

;

, (2.2.6.1.18)

где - площадь растянутого бетона в сечении;

; (2.2.6.1.19)

- диаметр продольной арматуры.

Определяем высоту растянутой зоны бетона (Рисунок 2.2.6.1.4):

, (2.2.6.1.20)

где - поправочный коэффициент, для тавровых сечений.

;

;

,

Расстояние между трещинами принимается в пределах ;

– условие выполняется.

Рисунок 2.2.6.1.4 - Растянутая и сжатая зоны приведенного сечения

; (2.2.6.1.21)

;

;

;

;

;

,

;

.

Условия выполняются.