1.3.5 Расчет на прочность сечений, нормальных к продольной оси

Расчет сечений, нормальных к продольной оси элемента, следует производить в зависимости от соотношения между значением относительной высоты сжатой зоны бетона , определяемой из соответствующих условий равновесия, и значением граничной относительной высоты сжатой зоны бетона .

Значение определяется по формуле

; (1.3.5.1)

.

Все значения , полученные в расчете, не должны превышать .

Метод предельного равновесия применим, когда .

Для определения значения относительной высоты сжатой зоны бетона опре- делим вспомогательные коэффициенты для различных значений моментов в пролетах и на опорах.

Для отрицательных значений изгибающих моментов для расчета требуемой площади арматуры берем моменты, которые возникают на расстоянии 0,25 пролета от опоры, а также моменты, которые возникают на опорах балки. Обозначим эти моменты и соответственно для первого и второго пролета (по номерам точек, между которыми лежат эти моменты), а также и для крайней и средней опоры (Рисунок 1.3.5.1).

Рисунок 1.3.5.1 - Изгибающие моменты во второстепенной балке

1.3.5.1 РАСЧЕТ НА ОТРИЦАТЕЛЬНЫЕ МОМЕНТЫ

При расчете на отрицательные моменты сжатая зона сечения будет находить- ся снизу, и сечение будет рассчитываться как прямоугольное шириной b = 200 мм (рисунок 1.3.5.1.1).

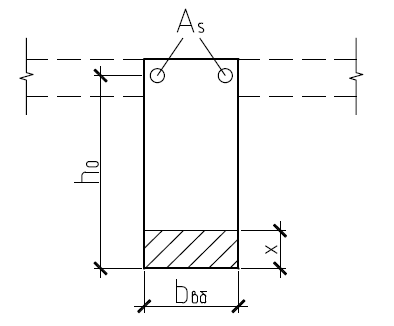
Рисунок 1.3.5.1.1 – Расчетная схема сечения

Для расчетных сечений определим значения по формуле (1.3.4.3):

;

;

0,205;

0,179;

Исходя из найденных значений , определим вспомогательные коэффициенты и относительную высоту сжатой зоны бетона . Все значения запишем в таблицу 1.3.5.1.1.

Таблица 1.3.5.1.1 – Значения коэффициентов , и относительной высоты сжатой зоны бетона

Для момента, кН м					; d
		0,988	0,025		157; 2d10
		0,956	0,089		157; 2d10
	0,205	0,884	0,231		402; 2d16
	0,179	0,901	0,199		402; 2d16

Все значения удовлетворяют условию . Также выполняется условие .

Определяем требуемую площадь поперечного сечения продольной арматуры для каждого значения изгибающего момента по формуле, мм²:

; (1.3.5.1.1)

;

;

;

;

Произведем проверку прочности сечения, то есть сравним действующий максимальный изгибающий момент с предельно допустимым.

Граничную высоту сжатой зоны определим по формуле:

; (1.3.5.1.2)

;

;

Тогда предельный изгибающий момент, который может воспринимать сечение:

; (1.3.5.1.3)

;

;

1.3.5.2 Расчет на положительные моменты

При расчете на положительные моменты полка расположена в сжатой зоне, к расчету принимаем тавровое сечение шириной полки , которое можно рассчитывать как прямоугольное, если высота сжатой зоны x не превышает высоту полки (Рисунок 1.3.5.2.1).

О пределим ширину полки при из условий:

;

.

К расчету принимаем меньшую из найденных величин, то есть 0,816 м.

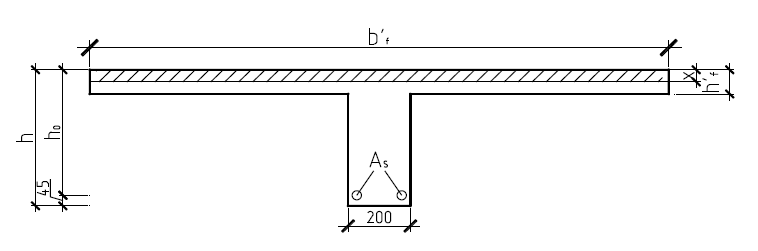
Рисунок 1.3.5.2.1 – Расчетная схема сечения

Рассчитаем сечения на действие двух максимальных моментов, которые возникают в пролетах второстепенной балки. Это моменты М_2‘ и М_7‘.

Максимальный момент, который может воспринимать сечение при высоте сжатой зоны равной высоте полки, кН∙м:

; (1.3.5.2.1)

;

.

57,25 .

Условие выполняется, граница сжатой зоны не выходит за пределы полки, и расчет будем выполнять как для прямоугольного сечения шириной .

; (1.3.5.2.2)

0,055;

0,044;

Исходя из найденных значений , определим вспомогательные коэффициенты и относительную высоту сжатой зоны бетона . Все значения запишем в таблицу 1.3.5.2.1.

Таблица 1.3.5.2.1 - Значения коэффициентов , и относительной высоты сжатой зоны бетона

Для момента, кН м
М2‘ = 57,25	0,055	0,972	0,057
М7‘ = 45,54	0,044	0,978	0,045

Все значения удовлетворяют условию . Также выполняется условие . Изменение сечения не требуется.

Требуемую площадь поперечного сечения продольной арматуры для каждого значения изгибающего момента определим по формуле (1.3.5.1.1):

;

;

Результаты расчетов сведем в таблицу 1.3.5.2.2.

Таблица 1.3.5.2.1 - Требуемая площадь поперечного сечения арматуры

Для момента, кН м			Устанавливаемая арматура
М2‘ = 57,25	0,972	384,7	2d16A500
М7‘ = 45,54	0,978	304,1	2d14A500

Произведем проверку прочности сечения, то есть сравним действующий максимальный изгибающий момент с предельно допустимым.

Граничную высоту сжатой зоны определим по формуле:

; (1.3.5.2.3)

;

;

Тогда предельный изгибающий момент, который может воспринимать сечение:

; (1.3.5.2.4)

;

;

> М_max

60,57>57,25 и 46,48>45,54.

Условие выполняется.

1.3.6 РАСЧЕТЫ НА ПРОЧНОСТЬ СЕЧЕНИЙ, НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ

Для расчета на прочность сечений, наклонных к продольной оси выделяем пролетные и приопорные участки (Рисунок 1.3.6.1). Необходимо рассчитать 5 участков (4-й и 6-й участки одинаковые), при этом 1-й,3-й и 4-й будут приопорными, 2-й и 5-й – пролетными.

Рисунок 1.3.6.1 – Эпюра поперечных сил во второстепенной балке

При расчете по прочности сечений, наклонных к продольной оси элемента, необходимо соблюдения следующих условий:

1) ;

2) ;

3) ,

где Q - максимальная поперечная сила на рассматриваемом участке, кН;

- прочность по бетонной полосе между наклонными сечениями, кН;

- прочность по наклонному сечению, кН;

- прочность бетона между хомутами, кН.

Первое условие было проверено нами в п.1.3.4, и будет соблюдаться для всех участков всех пролетов.

В условии 2:

,

где - поперечная сила, воспринимаемая бетоном в наклонном сечении, кН;

- поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении, кН;

Для поперечного армирования необходимо выполнение условия:

, (1.3.6.1)

где – диаметр поперечных стержней каркаса;

– диаметр продольных стержней.

.

Принимаем класс .

П ри расчете пролетных участков (2-й и 5-й) будем полагать, что поперечная сила воспринимается только бетоном, а поперечную арматуру будем устанавливать конструктивно согласно требований:

→ ;

;

принимается кратным 50 мм в сторону уменьшения.

.

;

; (1.3.6.2)

кН;

Кроме того необходимо, чтобы выполнялось и условие 3. Таким образом принятый шаг поперечной арматуры не должен превышать допускаемый:

;

; (1.3.6.3)

.

250мм < 704 мм – условие выполняется.

Длину пролетного участка определим графически (Рисунок 1.3.6.1).

При расчете приопорных участков (1-й, 3-й и 4-й) поперечная арматура будет учитываться в расчете:

;

Также для поперечной арматуры необходимо соблюсти следующие конструктивные требования:

→ ;

;

, (1.3.6.4)

где - максимальная поперечная сила на участке, кН.

,

Выбираем наименьшее значение кратно 50 мм.

.

Произведем проверку прочности приопорного участка с принятым армированием. Для этого определяем интенсивность хомутов:

, (1.3.6.5)

где n – количество каркасов (n=2);

.

Для учета поперечной арматуры в расчете проверяем выполнение условия:

. (1.3.6.6)

.

50,4 > 40,5 – условие выполняется, значит учитываем поперечную арматуру.

Находим длину проекции опасного сечения:

, (1.3.6.7)

где – условный момент.

; (1.3.6.8)

кН·м;

.

Должно выполняться условие:

,

,

.

; (1.3.6.9)

кН;

; (1.3.6.10)

;

; (1.3.6.11)

кН.

Условие выполняется.

3 участок:

→ ;

;

,

Выбираем наименьшее значение кратно 50 мм.

. Поскольку 150 мм не прошло по условию .

Произведем проверку прочности приопорного участка с принятым армированием. Для этого определяем интенсивность хомутов:

,

где n – количество каркасов (n=2);

.

Для учета поперечной арматуры в расчете проверяем выполнение условия:

.

.

75,6 > 40,5 – условие выполняется, значит учитываем поперечную арматуру.

Находим длину проекции опасного сечения:

,

где – условный момент.

;

кН·м;

.

Должно выполняться условие:

,

,

.

;

кН;

;

;

;

кН.

Условие выполняется.

4 участок:

→ ;

;

,

Выбираем наименьшее значение кратно 50 мм.

. Поскольку 150 мм не прошло по условию .

Произведем проверку прочности приопорного участка с принятым армированием. Для этого определяем интенсивность хомутов:

,

где n – количество каркасов (n=2);

.

Для учета поперечной арматуры в расчете проверяем выполнение условия:

.

.

75,6 > 40,5 – условие выполняется, значит учитываем поперечную арматуру.

Находим длину проекции опасного сечения:

,

где – условный момент.

;

кН·м;

.

Должно выполняться условие:

,

,

.

;

кН;

;

;

;

кН.

Условие выполняется.

1.3.7 КОНСТРУИРОВАНИЕ ВТОРОСТЕПЕННОЙ БАЛКИ С АНКЕРОВКОЙ ОБРЫВАЕМОЙ АРМАТУРЫ

Арматурные каркасы во второстепенной балке выполняют симметричными. Приведем схему армирования второстепенной балки, с необходимыми разрезами и сечениями (Рисунок 1.3.7.1).

Рисунок 1.3.7.1 – Армирование второстепенной балки

Для дальнейшего конструирования необходимо построить эпюру материалов, то есть область, ограниченную прямыми линиями, обозначающими моменты, которое может воспринимать сечение при данном армировании.

Для того, чтобы условие прочности соблюдалось везде, необходимо, чтобы эпюра моментов не выходила за контуры эпюры материалов. Для этого найдем моменты, которые может воспринимать сечение с данной арматурой по формуле:

; (1.3.7.1)

Высоту сжатой зоны находим по формуле (1.3.5.1.2).

Для стержней, воспринимающих положительные изгибающие моменты, за b принимаем ширину полки как в формуле (1.3.5.2.3).

Тогда:

;

;

;

;

кН·м;

кН·м;

кН·м;

кН·м;

Строим эпюру материалов (Рисунок 1.3.7.2).

Рисунок 1.3.7.2 - Эпюра материалов

Как видно из эпюры, арматура и бетон воспринимают все возникающие изгибающие моменты по всей длине балки.

Д ля стержней с диаметрами d₅ и d₆ необходимо определить величину анкеровки W. Она зависит от диаметра обрываемых стержней. Если точка теоретического обрыва попадает на приопорный участок, то

,

,

,

где - диаметр обрываемых стержней;

- базовая длина анкеровки, м.

, (1.3.7.2)

где и - площадь поперечного сечения обрываемого стержня и периметр его сечения соответственно;

- расчетное сопротивление сцепления арматуры с бетоном, для горячекатаной арматуры периодического профиля диаметром до 32 мм .

;

Положение точек теоретического обрыва принимаем на расстоянии четверти пролета от опоры. Поэтому и величину анкеровки отсчитываем от четверти пролета.

Величину анкеровки принимаем W = 258 мм.

2 Сборный вариант плоского перекрытия с балочными плитами

2.1 Компоновка и выбор варианта

2.1.1 Компоновка вариантов

Рассмотрим три варианта перекрытия:

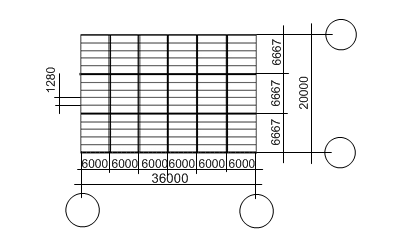
Рисунок 2.1.1.1 – Первый вариант перекрытия

Рисунок 2.1.1.2 – Второй вариант перекрытия

Рисунок 2.1.1.3 – Третий вариант перекрытия

Таблица 2.1.1.1 – Варианты перекрытия

Вариант	Плиты					Ригель
	nn	lп (мм)	nпр	bп (мм)	nр		lр (мм)
1	6	6000	5	1280	3		6667
2	7	5143	5	1280	3		6667
3	6	6000	6	1067	3		6667

Пролет ригеля вычисляется по формуле:

; (2.1.1.1)

где B – ширина здания, м;

- количество пролетов ригелей;

м;

Пролет плиты вычисляется по формуле:

; (2.1.1.2)

где L – ширина здания, м;

- количество пролетов плит;

м;

м;

Ширина плиты вычисляется по формуле:

; (2.1.1.3)

0,4 – ширина колонны, м;

- количество плит по 1 ригелю;

м;

м;

2.1.2 Сравнение и выбор варианта

Варианты сравниваются на основании количества используемых элементов.

Таблица 2.1.2.1 – Сравнение вариантов

Конструкции	Варианты
	1	2	3
Колонны	10	12	10
Ригели	15	18	15
Плиты	90	105	108
Вкладыши	12	14	12
Всего:	127	149	145

На основании проведенного сравнения вариантов самым экономичным является первый вариант перекрытия.