§4 Свойства волн де Бройля.

1)Так как волны де Бройля – волновые процессы , то все характеристики присущие волнам, можно применить к волнам де Бройля.

A, ω, ν, фаза, пространственные координаты x,y,z, и время t.

Свойства отличаются от реальных волн:

2)Фазовая скорость – скорость распределения в пространстве фазы волны.

V~C для релятивистской частицы.

Vфаз = ω / k

ω - угловая частота, k - волновое число

= 2Pi ν λ/2Pi = ν λh/h = h ν / p

Т.к. по де Бройлю λ = h/p, λ/ h=p

h ν = ε – энергия фотона или кванта

Vф = E/p = mC²/mV = С²/V V<C

Vф > C

СТО – специальная теория относительности. Отличительное свойство, нехарактерное для других волн.

3) Групповая скорость – равно скорости с которой распространяются в пространстве группы волн.

Групповая скорость Vгр=U – скорость амплитуды группы волн.

Vгр = U = d(ωħ)/d(ħk) = dE/dP

E² = E₀² + p²C²

U = d(sqr(E₀² + p²C²))/dp = 2pC²/2sqr(E₀² + p²C²)= pC²/E = pC²/mC²= p/m = mV/m = Vчаст=U

U=Vчаст

=> любую частицу можно представить в виде волнового пакета.

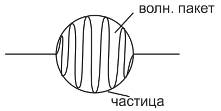
4)Дисперсия волн де Бройля

Дисперсия – зависимость фазовой скорости от длины волны.

Vф=f(λ)

В вакууме все реальные волны с различными длинами волн распространяются с одинаковой скоростью, те в вакууме нет дисперсии. ε = 1 (в вакууме.)

Среды с ε > 1 диспергируют.

Рассмотрим волны де Бройля:

Vф = ω / k = E/p = (E₀² + p²C²)/p = sqr((E₀² + p²C²)/p²) = sqr((E₀/ p²)+ C²)

λ =h/p => p = h/ λ

Vфаз = sqr((E₀² λ² / h²)+ C²) = f (λ) - не зависит от среды

волн де Бройля наблюдается дисперсия даже в вакууме.

5)Волны де Бройля и второй постулат Бора. (правило квантования орбит)

Le (момент импульса орбит) = mVr = nħ – правило квантования орбит

ħ = h/2Pi , n=1,2,3… ,бесконечность - квантовое число

mVr = nh/2Pi

2PirmV = nh mV=p

2Pirh/ λ = nh

2Pir = n λ

C точки зрения гипотезы де Бройля 2й постулат Бора:

стац. Орбитами электрона в атоме называются такие орбиты на длине которых укладывается целое число волн де бройля.

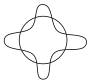n=4

§5 Соотношение неопределенностей Гейзенберга.

1)Разрыв однозначных связей между p и X в квантовой механике

Квантовая механика – особенность движения микрочастиц.

Микрочастицы – мелкие массы

В классической физике при движении классической мкч всегда наблюдается однозначная связь между импульсом этой частицы и ее координатами

В квантовой физике:

∆x стремится к 0:

λ определено точно.

∆P = 0

Положение объекта любое.

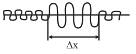
∆x!=0, λ определено не точно.

∆P не точно, ∆P !=0,

∆x стремется к 0: λ невозможно определить, P не точно, ∆P стремится к бесконечности

отсутствие траектории обусловлено волновым свойством.

2) Соотношение неопределенностей импульса и координат.

{∆x∆P_x>= ħ

∆y∆P_y>= ħ

∆z∆P_z>= ħ}

Произведение неопределенности координат на неопределенность импульса (?) не может быть менее ħ

3) Соотношение неопределенностей энергии и времени.

∆E∆t>= ħ

Разброс значений операции

E в атоме водорода

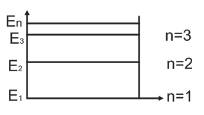
n=1

∆t стремится к бесконечности

∆E∆t= ħ

∆E = ħ/∆t = 0

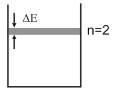
n=2

∆t = 10 ^–8 c

∆E= 10 ^{– 34} / 10 ^{– 8} = 10 ^{– 26}Дж

4)философские толкования

Одновременно точно импульс и координаты у мкч определить нельзя

§6 Волны де Бройля и волновая функция.

1.Формула Эйлера и комплексная формула записи волн.

S (x,t) = aCos (ωt – kx +σ)

ωt – kx + σ = α

Формула Эйлера: e^{+-i α} = Cos α +- iSin α

Для p – x iSin α = 0

aCos α = a e^{+-i α}

S(x,t) = a e^{+-i α}

2.Волновая функция и волна де Бройля

Пси функция обусловлена колебанием волны в пространстве

Ψ(x,t) = a e^{+-i α}

Ψ(x,t) = a e^{+-i (ωt – kx +σ)} = ae ^{+-i σ} e^{+-i (ωt – kx)}

ae ^{+-i σ} =A

ωt – kx = (Et - px)(1/ ħ)

Ψ(x,t) = Ae^{-i(1/ ħ) (Et - px)} для свободной мкч