§3 Опыты Франка и Герца. (1913)

Термо-электронная эмиссия.

Сетка положительно заряжена.

Подается напряжение (- + - +)

Катод-сетка: ускоряющее напряжение в промежуток

Сетка – Анод: наоборот тормозящее напряжение о,5 В

Атом ртути ₈₀ Hg ²⁰⁰

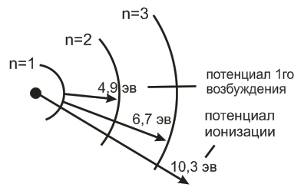
Потенциал ионизации – разность потенциалов которую должен пройти сторонний электрон чтобы при соударении с атомом выбить из него электрон. U эВ

Частота излучения та, с которой колеблется электрон.

Частота вращения = частоте излуч.

Вольтамперная характеристика из опытов Франка и Герца :

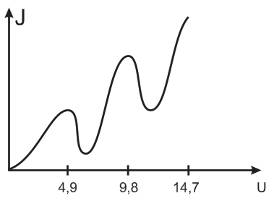
1е возрастание: ток растет тк растет U чем больше потенциал тем больше электронов.

1й спад: электрон сталкивается с электроном ртути, при этом столкновении до U=4,9 соударения упругие, начиная с 4,9 соударения неупругие (у сетки)

Далее увеличиваем U, электрон отдавший энергию находится в ускор. Поле, поэтому преодолевает напряжение, график снова растет

И т.д.

Передача энергии электроном не всегда происходит, тк атом в любом количестве энергию у электрона не принимает.

При передаче энергии есть свечение.

§4 Теория атома водорода и водородоподобных ионов по Бору.

1.Эксперементальные факты, объясняемые теорией Бора:

а- размер атома водорода r=53 пм

б- энергия ионизации атома водорода Eи = 13,6 эв

Eи – энергия бомбардирующего электрона достаточная для того чтобы при соударении выбить электрон из атома.

Потенциал ионизации Uи – разность потенциалов которую должен пройти бомбардирующий электрон чтобы приобрести энергию достаточную для ионизации атома.

Eи = eUи

в- закономерность линейчатого спектра.

1/λ = R(1/n_i²-1/n_j²)

2. Радиусы орбит атомов.

{ ke²/r² = mV²/r классическая модель

mVr = nћ } – квантовая модель

k = 1/4Piε0 n=1,2,3…

момент импульса кратен ћ

kme² r³/r² = mV²m r³/r = m²V² r²

m²V² r² = n²ћ²

kme² r = n²ћ²

r_n = n²ћ²/kme² - закон квантования

n=1 r₁= ћ²/kme²

r₁=(1,05*1,05*10^-68)/(9*10⁹*9*10^-31*2,56*10^-38) = 53*10^-12 м

[r]=дж²*с²*Ф/м*кг*кл² = м

Кл/Ф = В*кл = дж

n₂=2 r₂=4r₁

n₃=3 r₃=9r₁

r_n=nr₁

3. Скорость электрона

признак водорода E=1 ?

V_n= ke²/ nћ

V₁= ke²/ ћ : n=1

V₁= (9*10⁹*2,56*10^-38)/(1,05*10^-34) = 2,2*10⁶ (м/с)

[V] = м*кл²/Ф*Дж*с = м/с

V_n = V₁ / n

4. Энергия электрона в атоме

E = - ke²/ 2r

E = T + U

E = - ke²km e²/2n² ћ ² = - k²me⁴/2n² ћ ²

E_n = - k²me⁴/2n² ћ ²

n = 1:

E₁ = (81*10¹⁸*9,1*10^-31*2,56*2,56*10^-76)/(2*1,05*1,05*10^-68*1,6*10^-15) = - 13,6 эв

[E] = м²*кг*кг⁴ / Ф² * Дж² * с² = Дж

E_n = E_{(бесконечности)} - E₁

E_{(бесконечности)} = 0

E_n = E₁ / n² n=1,2,3… - главное квантовое число

5. Закономерность линейчатых спектров.

1/λ = R(1/n_i²-1/n_j²)

По Бору:

hυ = Ej – Ei = - k²me⁴/2n_j² ћ ² – (- k²me⁴/2n_i² ћ ² ) = k²me⁴/2 ћ ² (1/ n_i² – 1/n_j²)

hυ = hC/ λ (?)

k²me⁴/2hCћ ² = (81*10¹⁸*9,110^-31*2,56*2,56*10^-76)/( 2*1,05*1,05*10^-68*6,62*10^-34*3*10⁸¹) = 1,1*10⁷ м^-1

6. Спектр атома водорода.

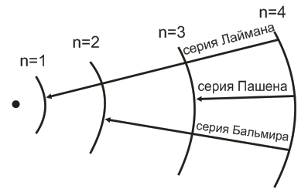
диаграмма уровней энергии в атоме водорода

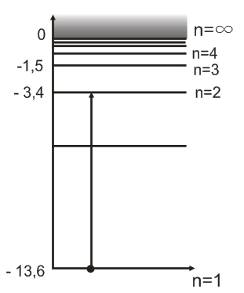
E _{первого возбуждения} = 10,2 эв

U _{первого возбуждения} = 10,2 эв

7. Магнитные моменты.

Гиромагнитное отношение

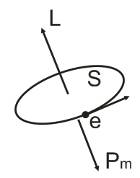
L = m [Vr] - вектор – механический момент

L = mVr

P_m = магнитный момент

P_m = JS = eVPir²/2Pir = eVr/2

J = eV/2Pir

P_m / L = eVr/2mVr = e/2m – гиромагнитное отношение

P_m = - Le/2m L= nћ

P_m = - e nћ / 2m

eћ / 2m = μ_Б = 0,9*10^-23 – магнетон Бора – минимальная порция магнитного момента в природе

P_m = n μ_Б

8. Водородные ионы.

z=1

{ kze²/r² = mV²/r классическая модель

mVr = nћ } – квантовая модель

r = n²ћ² / kmze²

V = kze² / nћ

En = k²mz²e⁴ / 2 n²ћ²

1/λ = z²R(1/n_i²-1/n_j²)

§6 Затруднения Теории атома водорода и водородоподобных ионов по Бору.

Решила много вопросов, объяснила эксперименты и тд.

Позже начали находить недостатки:

1)непоследовательность

{mVr = nћ - квантовое товое положение

kze²/r² = mV²/r } классическое положение

теория не могла долго существовать и была переходной.

• Не смогла объяснить интенсивность спектральных линий.

• Справедлива только для водородоподобных атомов и не работает для атомов, следующих за ним в таблице Менделеева.

• Теория Бора логически противоречива: не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно — уравнение движения электрона — классическое, другое — уравнение квантования орбит — квантовое.

Элементы Квантовой Механики.

Введение. История создания квантовой механики.

В ее основу легли 2 факта: теория Бора и дуализм света.

1924-1926

Шрединг, Гейзинберг, Борн

Дуализм света (одновременно электро-магнитная волна и поток фотонов):

{ε=hν = hC/λ=ħω -энергия фотона

P = hν/C = h/λ = ħk}-импульс фотона

k=2Pi/λ

дуализм света – объективный закон природы.

Глава 4. Волновые свойства микрочастиц.

§1 Гипотеза Луи де Бройля. 1923г.

Утвердилось учение о дуализме. ЛдБ предположил что дуализм присущ всей материи – электронам, протонам, нейтронам...

есть частица, перемещающаяся со скоростью V значит она обладает импульсом P и ее движение характеризует волна. О природе волн де Бройля было много споров. Это математический аппарат для описания движения частиц.

λ=h/p ω= ε/ħ

если частица свободная, нерелятивистская, T<<m₀C²

1)cвободная U(x)=0 T_кин=p²/2m

λ=h/sqr(2mT_кин) p=sqr(2mT_кин)

2)cвязанная (в силовом поле)

U(x)!=0

E=T_кин+U(x)

T_кин=E-U(x)

λ=h/sqr(2m(E-U(x)))

Если частица релетявистская, T~m₀C² - энергия покоя

λ=h/p

E²=E0²+p²C²

p²C² = E^{2 –} E0²

E= mC² E₀ = m₀C²

p² = (E - E₀)(E + E₀)/C²=T(2m₀C²+T)/ C²

λ=hC/sqr(T(T+2m₀C²))

чуваки эту ляляку встретили негативно, только эксперименты убедили их:

определить λ шарика m=1г движущегося со скоростью V=1см/с

λ = h/mV = (6,62 10^-34 дж с)/(10 ^-3 10 ^-2 м/с)=6,62 10 ^-29 м

длина волны настолько мало что отсутствуют методы определения такой длины волны

определим λ для электрона в атоме водорода, V=10⁶ м/с

λ = h/mV = (6,62 10^-34 дж с)/(9,1 10 ^-31 10 ⁶ м/с) ~ 0,7 нм – частота рентгеновского излучения

для рентгеновских лучей наблюдается дифрагция на монокристаллах.