3.Квантовые числа
1)Главное квантовое число n=1,2,3…
E = - (1/n2) (k2me4/2ћ2)
2) Орбитальное квантовое число l=0,1,2,…,(n-1)
Характ. Орбит. Момент.
L=sqr(l(l+1)) ћ, L=[r,P] (вект), p=mV(вект)
3) магнитное квантовое число me= 0, +-1,+-2,…,+-l
Lz = me ћ
Состояние электрона в атоме
Таблица:
n l me сост
1 0 0 1S
2 0|1 0|-1 0 1 2S|2p
3 0|1|2 0|-1 0 1|-2 -1 0 1 2 3S|3p|3d
При одном и том же n может быть несколько состояний. Состояние электрона с одинаковой энергией называются вырожденными.
Кратность вырождения N
n, l – n значений m=(2n+1)
N=∑(от эль до n-1)(2l + 1) = 1+3+5…
N=(1+2n-2+1)n/2=n2
4.Спектр атома водорода. Правило отбора.
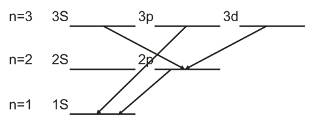
∆l = +-1
∆me = 0,+-1
Правило отбора отражает закон сохранения импульса.
Серия лаймана (n,p --- 1S), n=2,3…
Серия Бальмира (nS --- 2p), (nd---2p), n=3,4
5.Сферич. Симметрич. Случай. (1s сост)
(1/r2)( ∂/∂r)(r2∂ ψ /∂r) + (1/r2Sinθ)(Sinθ∂ ψ /∂θ) + ( 1/r2Sinθ)( ∂2 ψ /∂ φ 2) + (2m /ħ2)(E + ke2/r) ψ =0
ψ (r,θ,φ)
∂ ψ /∂ θ = 0 ∂ ψ /∂ φ = 0
(1/r2)( ∂/∂r)(r2∂ ψ /∂r) + (2m /ħ2)(E + ke2/r) ψ =0
(1/r2) 2r ( ∂ ψ /∂r) (1/r2) r2∂ 2ψ /∂r2 + (2m /ħ2)(E + ke2/r) ψ =0
∂ 2ψ /∂r2 + (2/r) ( ∂ ψ /∂r) + (2m /ħ2)(E + ke2/r) ψ =0
ψ = e -ar
∂ ψ /∂r = -a ψ
∂ 2ψ /∂r2 = a2 ψ
a2 ψ – (2a ψ/r) + (2m /ħ2)(E + ke2/r) ψ =0
a2 – (2a /r) + (2m /ħ2)(E + ke2/r) =0
(a2 + 2mE /ħ2) + (2/r)( kme2/ћ2 -a) =0
kme2/ћ2 -a =0
a = kme2/ћ2 a=1/r
ψ = e -2/r
a2 + 2mE /ħ2 =0
E= - ħ2a2/2m = - ħ2k2m2e4/2mћ4 = - k2m2e4/2ћ2
6. Местонахождение электрона в атоме в 1s состоянии
ψ = Ae -r/r1 A – нормирующий множитель
(интеграл от 0 до бескон.)( A2e -2r/r1)dV = (интеграл от 0 до бескон.)( A2e -2r/r14Pir2)dr = 1
dV=4Pir2dr
4Pi A2(интеграл от 0 до бескон.)( r2 e -2r/r1) = 1
A2 Pir13=1
A = sqr (1/ Pir13)
ψ = e -r/r1/ sqr ( Pir13)
dW = | ψ 2|dV
dW = (e -2r/r1/ ( Pir13)) 4Pir2dr – вероятность обнаружить электрон в dr
Радиальная плотность вероятности:
ρ(r) = dW/dr = (1/ Pir13) (e -2r/r1) 4Pir2
r стремится к 0, ρ(r) стремится к 0
r стремится к бесконечности, ρ(r) стремится к 0
∂ ρ(r) /∂ r = 0
(4/ r13)((-2/ r1) (e -2r/r1)r2 + 2r(e -2r/r1))=0
(4/ r13)( 2 r e -2r/r1)(1 – r/r1) = 0
1 – r/r1 = 0
r = r1 – максимальный радиус плотности вероятности
Сравнение с теорией Бора
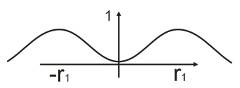
ψ = e -r/r1/ sqr ( Pir13)
§8 Магнитные свойства и спин электрона.
Энергетические уровни электрона в атоме расщепляются изза того, что электрон имеет магнитный момент.
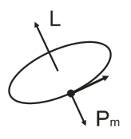
L = [r, mV] – момент импульса
Pm = JS
Pm / L = l/2m
В квант механике
L= sqr(l(l+1)) ħ
L=n ħ по Бору
(l/2m) ħ sqr(l(l+1))
----------
Pm = - eL/2m (вект) – орбитальным магнитный момент
e/2m – гиромагнитное отношение
по квантово-механической модели:
L = sqr(l(l+1)) ħ – закон квантования магнитных моментов
Pm = sqr(l(l+1))μб
μб = e ħ /2m – минимальная порция магнитного момента в природе
Запустили в состояние 1S => L=0
Если L=0 атомы прошли и с МП(магнитное поле?) не взаимодействовали. НО
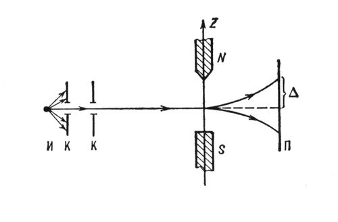
Опыты Штерна и Германа
F = μ (∂B/∂x)Cosα
Cosα = (μ, B) (вект)
1S n=1 l=0 me=0 Pm=0
Опыт состоял в следующем: пучок атомов серебра пропускали через сильно неоднородное магнитное поле, создаваемое мощным постоянным магнитом. При прохождении атомов через это поле, в силу обладания ими магнитных моментов, на них действовала зависящая от проекции спина на направление магнитного поля сила, отклонявшая летящие между магнитами атомы от их первоначального направления движения. Причём, если предположить, что магнитные моменты атомов ориентированы хаотично (непрерывно), то тогда на расположенной далее по направлению движения атомов пластинке должна была проявиться размытая полоса. Однако вместо этого на пластинке образовались две достаточно чёткие узкие полосы, что свидетельствовало в пользу того, что магнитные моменты атомов пучка принимали лишь два определённых значения, что подтверждало предположение квантово-механической теории о квантовании магнитного момента атомов.
Гипотеза об электронном спине
У электрона есть собственный магнитный момент
Ls – спиновый механический момент (момент импульса)
Pms – спиновый магнитный момент
1925 Гаудсмит и Уленберг (1я теория. не прошла.)
S=1/2 ms = +-1/2
Ls = sqr(S(S+1)) ħ Ls = sqr(3) ħ /2
S – спиновое квантовое число
|Pms| = e Ls / m = (e ħ / m) sqr(S(S+1)) = sqr3 μб
Проекция на выбранное направление z:
Pmsz = e Lsz / m = e sqr3 ms ħ / m 2 = +- μб
Lsz = ms ħ
Электрон движется по орбите. У него будто маленькая магнитная стрелочка.
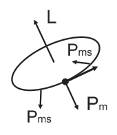
Объяснение расщепления спектральных линий:
Без учета спина:
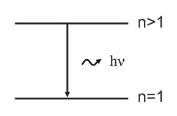
С учетом спина:
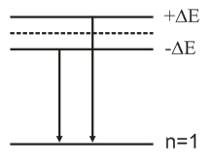
Уровень расщепляется, линии носят дублетный характер
Тонкая структура линий.