§5 Микрочастица в потенциальной яме конечной глубины.

1. U(x) = {U₀, x<=0, x>=L

0, 0<x<L}

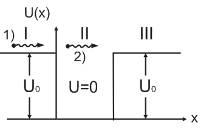
2.Уравнение Шредингера

I,III U(x) = U₀

(- ħ²/2m) (d² ψ /dx² ) + U₀ ψ = E ψ

(d² ψ /dx² ) + (2m (E - U₀) ψ/ ħ²)=0

k_1,3 = sqr (2m (E - U₀) / ħ²)

(d² ψ /dx² ) + k_1,3² ψ = 0

II

(- ħ²/2m) (d² ψ /dx² ) = E ψ

(d² ψ /dx² ) + (2m E ψ/ ħ²)=0

k₂ = sqr (2m E / ħ²)

(d² ψ /dx² ) + k₂² ψ = 0

Решение:

ψ _I(x) = A₁ e ^ik1,3x + B₁ e ^–ik1,3x

ψ _II(x) = A₂ e ^ik2x + B₂ e ^{- ik2x}

ψ _III(x) = A₃ e ^ik1,3x + B₁ e ^–ik1,3x B₃=0

Анализ решения:

1)E> U₀ (микрочастица свободная)

k_1,3 и k₂ – действительные числа

k_1,3 > k₂ λ = 2Pi/k λ_1,3 < λ₂

рис*

Энергия не квантуется

2)E< U₀

k₂ - действительное число

k_II3 – мнимое число k_1,3 = ik

Решение:

ψ₁(x) = A₁ e ^-kx + B₁ e ^kx A₁ e ^–kx не удовлетворяет условию конечности при x<0 - сокращаем

ψ₂(x) = A₂ e ^ik2x + B₂ e ^-ik2x

ψ₃(x) = A₃ e ^-kx

пси функция удовлетворяет только при определенных значениях E. E квантуется

спектр энергий дискретный

E= n² Pi²ħ²/2mL²

В потенциальном ящике n – бесконечно

В потенциальной яме n - конечно.

Вероятность обнаружить мкч:

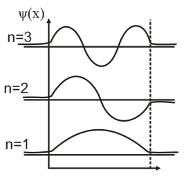
Мкч можно обнаружить в I и III области.

§6 Квантово-механический осциллятор

1.Гармонический осциллятор

- точка или система точек, совершающая гармонические колебания.

X=ACosωt

F = - c x c – коэффициент упругости

Сила упругая или квази упругая

F= - grad U

U = cx²/2

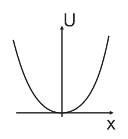
2.Классический гармонический осциллятор

(рисунок шарик на пружинке)

md²x/dt² = -cx F_y = -cx

d²x/dt² + cx/m =0 c/m=ω₀²

d²x/dt² + ω₀²x = 0

решение: x = ACos(ω₀ + φ₀) - смещение от положения равновесия

V = dx/dt = - A ω₀Cos(ω₀t + φ₀)

T = mV2/2 = (m A² ω₀² / 2) Sin²(ω₀t + φ₀)

U = cx²/2 = (cA²Cos²(ω₀t + φ₀))/2

U = (m A² ω₀² Cos²(ω₀t + φ₀)) / 2

E = T + U = m A² ω₀² / 2

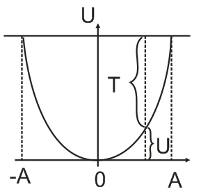
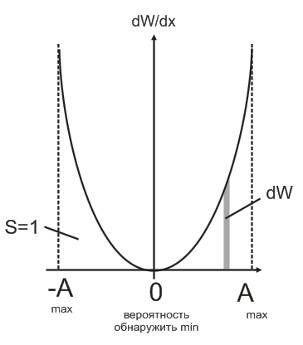
-A, A – точки поворота – U=E

Вероятность местонахождения

dW/dx – плотность вероятности

(интеграл от –A до А)(Wdx) = 1

3.Квантово-механический осциллятор

Электрон в атоме, атом в кристалле… колеблющаяся частица ???

Уравнение Шредингера

(- ħ²/2m) (d² ψ /dx² ) + (cx²/2) ψ = 0

Решение: ψ = A_n e^{αx^2}

A_n – нормирующий множитель

Пси функции удовлетворяют стандартным естественным условиям не при всех E

Энергия осциллятора

E = (2n + 1) ħ ω₀/ 2 n = 0,1,2,3…

ħ ω₀ – расстояние между уровнями

Энергия меняется по параболическому закону

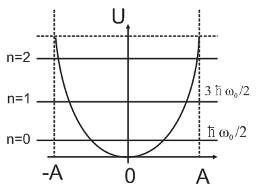
Emin, n=0: Emin = ħ ω₀ /2

n=1: E₁ = 3ħω₀ /2

n=2: E₂ = 5ħω₀ /2

Классический гармонический осциллятор может находится в состоянии покоя, механический – нет.

ħω₀ – энергия нулевых колебаний

нулевые колебания – колебания которые квантово-механический осциллятор совершает при t=0

ставили опыты. Интенсивность рассеяния при определенных условиях минимальна. При t=0 колебания есть, иначе было бы нарушение ∆x∆P_x>= ħ (соотношение неопределенности импульса и координат)

доказано при наблюдении рассеивания света на монокристалл.

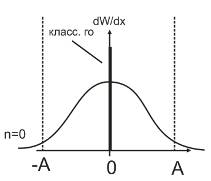
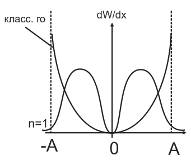
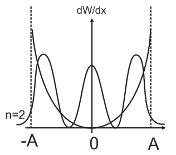
С возрастанием n, квантово-механический осциллятор стремится к классическому.

§7 Квантово-механическая модель атома.

1.Качественное рассмотрение

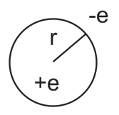
r = n²ћ²/kme²

II обл

T = ke²/2r U=-ke²/r

E = T+U=-ke²/2r

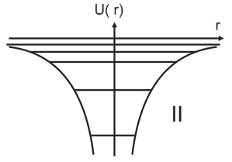
r стремится к бесконечности, U стремится к 0

r стремится к 0, U стремится к - бесконечности

I обл E>0, принимает любые значения

II обл E<0

2. Уравнение шредингера для электрона в атоме водорода

U=-ke²/r

(- ħ²/2m)∆ψ + (-ke²/r) ψ = E ψ

∆ψ + (-2m /ħ²)(E + ke²/r) ψ = 0

Сферические координаты

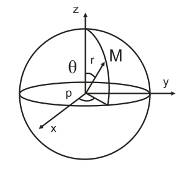
M(r,θ,φ)

X = 2Sinθ Sinφ

Y=2Sinθ Cosφ

Z=rCosθ

∆ = (1/r²)( ∂/∂r)(r²∂/∂r) + (1/r²Sinθ)(Sinθ∂/∂θ)+( 1/r²Sinθ)( ∂²/∂φ²)

(1/r²)( ∂/∂r)(r²∂ ψ /∂r) + (1/r²Sinθ)(Sinθ∂ ψ /∂θ) + ( 1/r²Sinθ)( ∂² ψ /∂φ²) + (2m /ħ²)(E + ke²/r) ψ = 0

Решение:

ψ (r,θ,φ)

1) E>0, при любых E

2)E<0

Уравнение решилось только при введении дополнительных параметров: n, L, m_e