40. Дискретное z-преобразование.

В теории импульсных систем для решения разностных уравнений используется дискретное преобразование Лапласа и его модификация - дискретное z-преобразование.

Преобразование Лапласа для непрерывной функции х(t):

X(р) = x(t) exp(-pt) dt. (6.2.3)

При переходе к дискретной функции x(kТ), заменяя интегрирование суммированием:

X(p) =T x(kT) exp(-pkT). (6.2.4)

Введем новую переменную z=exp(pt):

X(z) =T x(kT) z^-k . (6.2.5)

Это уравнение представляет собой дискретное преобразование Лапласа, в котором выражение

X(z) = x(kT) z^-k . (6.2.6)

называется z-преобразованием. Оно лежит в основе метода решения разностных уравнений. Дискретное преобразование Лапласа X(z) отличается от z-преобразования наличием нормирующего множителя Т. При анализе дискретных систем z-преобразование позволяет перейти от разностных уравнений к алгебраическим и существенно упростить анализ динамики дискретных систем.

В выражении (6.2.6) функция х(kТ) называется оригиналом решетчатой функции, a X(z) – ее изображением. Для обратного перехода от изображения к оригиналу (для нахождения исходной решетчатой функции по ее изображению) используется обратное z-преобразование:

x(kT) = (1/2j) ∮ X(z) z^k-1 dz.

Корни p_i характеристического полинома непрерывной системы связаны с корнями z_i характеристического полинома эквивалентной дискретной системы соотношением

41. z_i = exp(Tp_i). (6.2.7)

В общем случае, отображение (6.2.7) неоднозначно, и нескольким различным значениям p_i может соответствовать одно и то же значение z_i. Взаимно-однозначное соответствие корней непрерывной и эквивалентной дискретной систем выполняется только при интервале дискретизации, удовлетворяющем теореме Котельникова-Шеннона.

42. Преобразование непрерывного сигнала в цифровой код.

выполняется амплитудно-цифровыми преобразователями (АЦП) и включает три операции: квантование сигнала по времени, квантование по уровню и кодирование. Квантование по времени заключается в измерении непрерывной величины х(t) в дискретные моменты времени t_k=kt, t=const, k=0, 1, 2,…, и осуществляется импульсным элементом - ИЭ. На выходе импульсного элемента получается решетчатая функция x(t_k).

Рис. 6.2.1.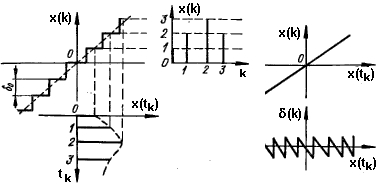

Процесс квантования решетчатой функции х(t_k) по уровню можно представить как прохождение сигнала х(t_k) через нелинейный элемент с многоступенчатой релейной характеристикой - квантователь по уровню КУ (рис. 6.2.1). В результате квантования по уровню точно измеренные значения сигнала х(t_k) заменяются приближенными ближайшими дискретными значениями х_k  x(k)  x(t_k). Шаг квантования _k, характеризует точность преобразователя.

Учет квантования по уровню приводит к необходимости рассмотрения нелинейных цифровых систем. Анализ систем упрощается, если элемент с многоступенчатой релейной характеристикой представить в виде параллельного соединения линейного усилительного элемента с коэффициентом K = 1, характеристика которого изображена на рис.6.2.1 справа, и нелинейного элемента с характеристикой (k), равной разности между линейной и релейной характеристиками. В этом случае квантованный по уровню сигнал можно представить, как сумму точного сигнала х(t_k) и добавочного сигнала (k), ограниченного по величине половиной ступени квантования:

Прежде чем сигнал х(k) поступает на цифровое вычислительное устройство (ЦВУ) системы, осуществляется его кодирование - преобразование в цифровой код х_ц(k). Если в ЦВУ используется двоичная система счисления, то с помощью кодирующего устройства К каждый импульс, поступающий с квантователя по уровню, преобразуется в двоичный цифровой код, соответствующий амплитуде этого импульса. Двоичные числа представляются в виде последовательности импульсов, разделенных интервалом времени . Каждому разряду двоичного числа отводится интервал времени ' на выставление кодов 0 или 1 (обычно отсутствие или наличие определенного уровня напряжения).

На ЦВУ числа могут поступать последовательным или параллельным кодом. В первом случае разряды числа идут последовательно друг за другом по одному каналу, как правило, начиная с младшего. Одно число от другого отделяется специальным маркерным импульсом. Минимальный интервал Т передачи числа равен n, где n - количество разрядов числа. При параллельном коде все разряды числа поступают одновременно по нескольким каналам, число которых равно числу разрядов. Так как при кодировании сигнала не происходит изменения информации, то передаточная функция кодирующего устройства равна единице.