ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ
ВВЕДЕНИЕ
Основные задачи управления (теории управления)
Теория управления – это наука, разрабатывающая и изучающая методы и принципы систем управления, а так же закономерности протекающих в них процессов.
Управление - это специально организованное воздействие на объект управления с целью получения результата.
Объект управления - это техническое устройство или процесс.
Задачи ТУ- анализ системы управления и ее синтез.
Анализ системы управления состоит в определении устойчивости и качества системы управления при закрепленной структуре и зафиксированных значениях настроечных параметров системы.
Синтез системы управления состоит в выборе такой структуры и таких значений настроечных параметров, при которых система управления удовлетворяет заданным требованиям по устойчивости и качеству управления.
Основные принципы управления.
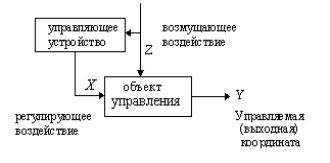
Принцип компенсации (управления по возмущению).
При управлении по возмущению управляющее воздействие вырабатывается управляющим устройством в зависимости от величины возмущения. Системы управления по возмущению являются разомкнутыми системами, так как в них отсутствует обратная связь. Управление по возмущению возможно в том случае, если возмущающее воздействие можно измерить. Системы, построенные по принципу компенсации возмущений, не могут компенсировать все возможные возмущения в объекте управления, так как все их практически невозможно измерить.
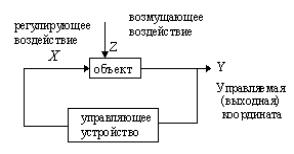
Принцип управления по отклонению(обратная связь).
При управлении по отклонению управляющее устройство изменяет управляющее воздействие при отклонении управляемой координаты от заданного значения независимо от причин, вызвавших это отклонение. Системы управления, построенные по этому принципу, являются замкнутыми. В этих системах трудно одновременно выполнить условия точности, устойчивости и высокого быстродействия.
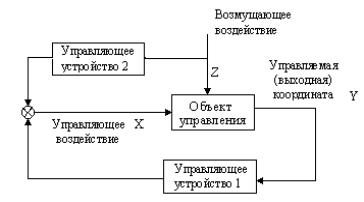
Комбинированные системы управления.
Сочетают оба рассмотренных выше принципа.В таких системах основное, наиболее сильное, измеряемое возмущение компенсируется специальным управляющим устройством, а устранение отклонения управляемой величины, вызванного другими не измеряемыми возмущающими воздействиями, осуществляется контуром управления с обратной связью.
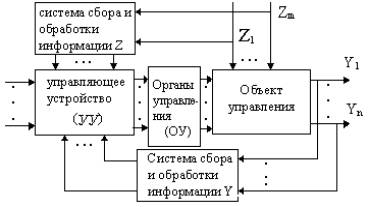
Основные виды систем управлений.
Системы стабилизации – в них Yзад = const. Y-управляемая(выходная) координата.
Следящие - в которых задание управляющему устройству изменяется в зависимости от какого либо другого параметра, то есть управляемая координата «следит» за изменением этого параметра.
Программные -в которых задание регулятору изменяется во времени по заранее заданной программе.
Пример структурной схемы одноконтурной системы управления
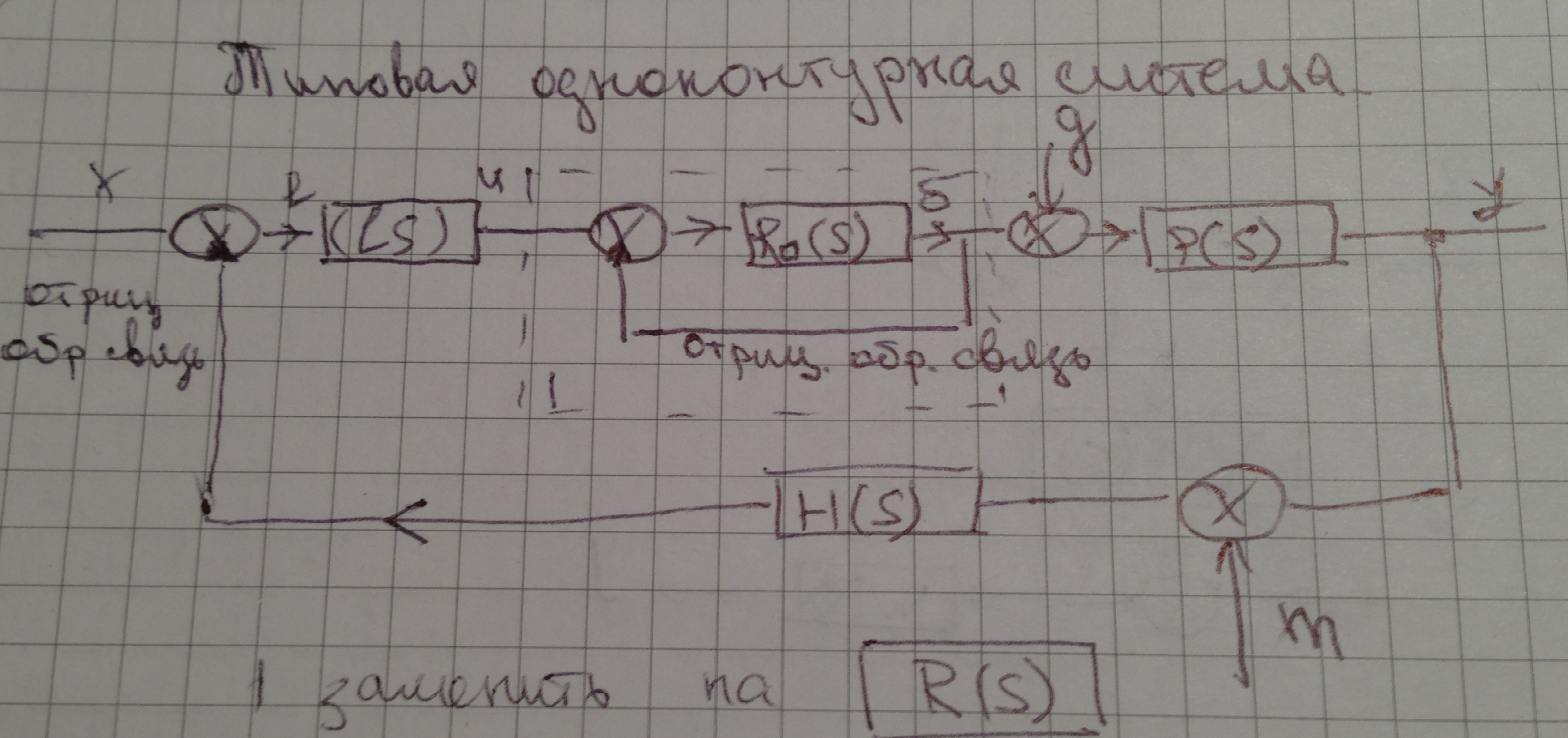
Виды регуляторов (pid регулятор)
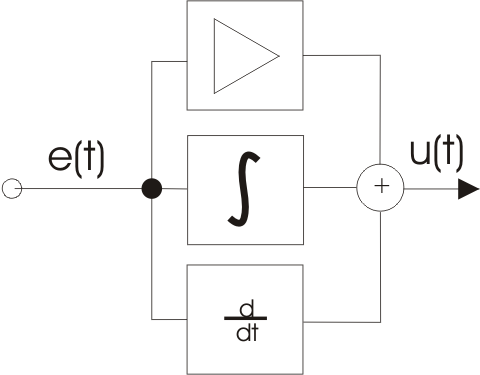
Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.
Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. П
Пропорциональная составляющая
Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.
Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Интегральная составляющая
Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.
Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям.
Дифференциальная составляющая
Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.
Пример модели регулятора с обратной связью (регулятор уровня), структурная схема, уравнение динамики (с пропорциональным регулятором), зависимость точности регулирования от величины коэффициента усиления
МОДЕЛИ ЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ И ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
Представление модели в виде дифференциального уравнения (ДУ) «вход-выход» n- го порядка и в пространстве состояний
Переходная функция
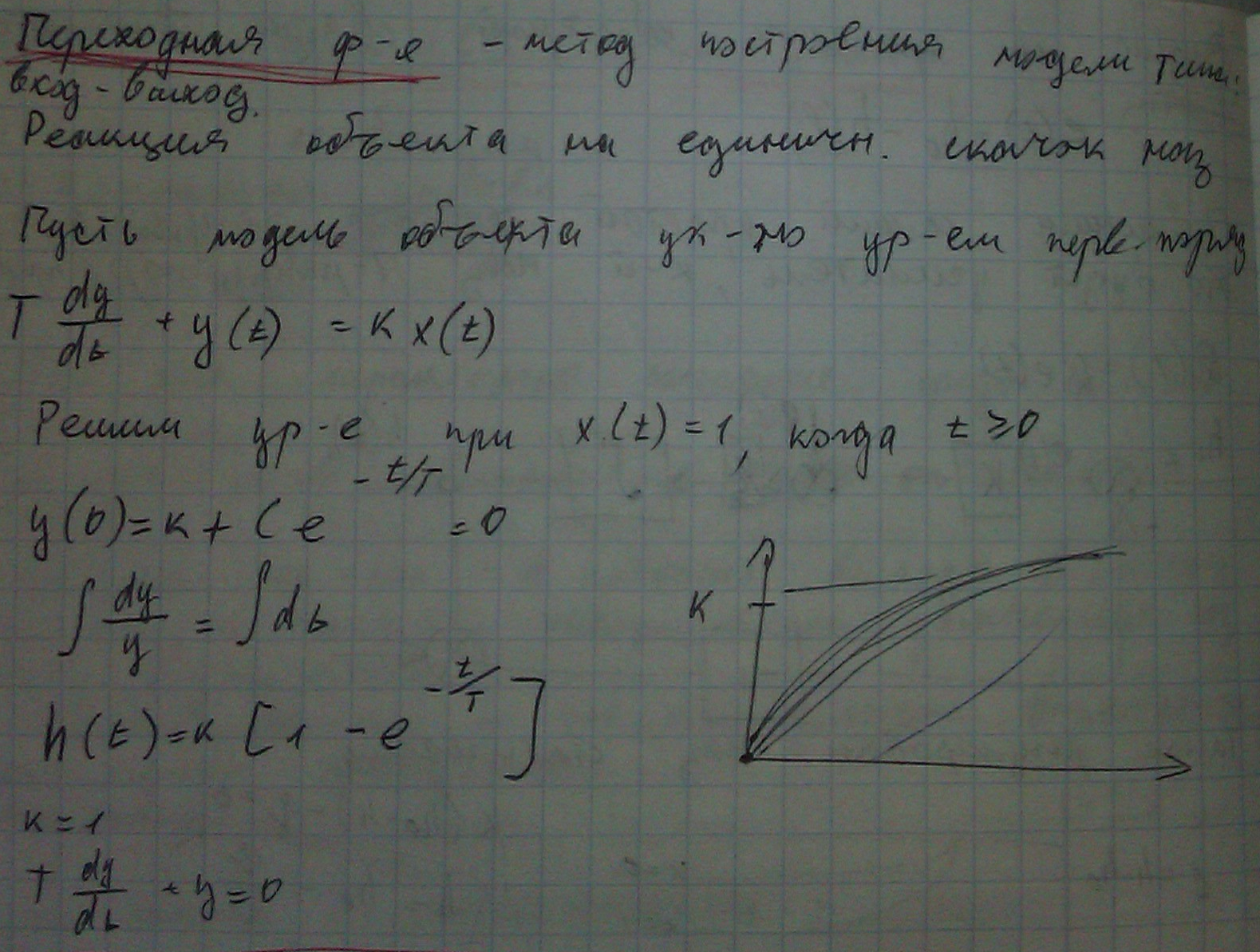
Импульсная характеристика (весовая функция)
Передаточная функция (пример линейного ДУ 2-го порядка)
Преобразование Лапласа
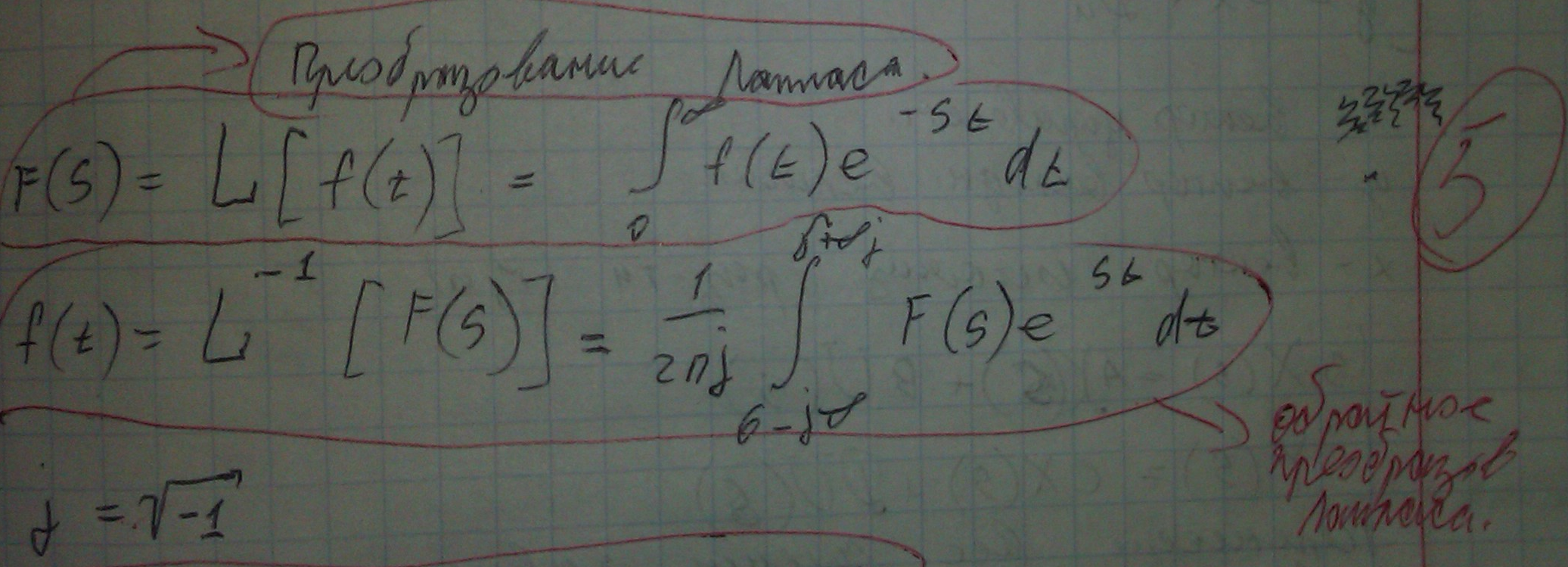
Свойства преобразования Лапласа, изображения дельта-функции (импульса), единичного скачка, экспоненты, производной, интеграла)
Передаточная функция линейного ДУ 2-го порядка
Пример преобразования Лапласа для уравнения 1-го порядка
Передаточная функция и пространстве состояний
Частотные характеристики (АЧХ и ФЧХ)
Фазо-частотная характеристика (ФЧХ) — частотная зависимость разности фаз между выходным и входным сигналами.
Для линейной электрической цепи, зависимость сдвига по фазе между гармоническими колебаниями на выходе и входе этой цепи от частоты гармонических колебаний на входе.
Часто ФЧХ используют для оценки фазовых искажений формы сложного сигнала, вызываемых неодинаковой задержкой во времени его отдельных гармонических составляющих при их прохождении по цепи
Определение ФЧХ
В теории управления ФЧХ звена определяется из равенства её тангенса отношению мнимой части АФЧХ к действительной:
Амплитудно-частотная характеристика (АЧХ) — функция, показывающая зависимость модуля некоторой комплекснозначной функции от частоты. Также может рассматриваться АЧХ других комплекснозначных функций частоты, например, спектральной плотности мощности сигнала.
АЧХ в теории автоматического управления
АЧХ в теории линейных стационарных систем означает зависимость модуля передаточной функции системы от частоты. АЧХ показывает во сколько раз амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на всём диапазоне частот.
На графике АЧХ по оси абсцисс откладывается частота, а по оси ординат отношение амплитуд выходного и входного сигналов системы. Обычно для частоты используется логарифмический масштаб, так как исследуемый диапазон частот может изменяться в достаточно широких пределах (от единиц до миллионов Гц или рад/с). В случае когда логарифмический масштаб используется и на оси ординат, АЧХ превращается в логарифмическую амплитудно-частотную характеристику. ЛАЧХ получила широкое распространение в теории автоматического управления в связи с простотой построения и наглядностью при исследовании систем управления.