6. Заключение.

Таким образом, рассмотрено вычисление первого и второго замечательных пределов. Введено понятие бесконечно больших функций и установлена их связь с бесконечно малыми. Следует отметить, что нельзя смешивать постоянное очень большое число с бесконечно большой функцией. Бесконечно малые и бесконечно большие функции находят большое практическое применение. Например, используя сравнение бесконечно больших величин, которое производится аналогично сравнению бесконечно малых, можно получить асимптотические формулы. Приведем без вывода одну из самых замечательных асимптотических формул - формулу Стирлинга/ Д. Стирлинг( 1692 - 1770) - английский математик / , позволяющую вычислять факториалы n! для больших чисел n :

n!  при n.

ЛЕКЦИЯ №

НЕПРЕРЫВНОСТЬ ФУНКЦИИ.

План.

1. Введение.

2. Определение непрерывности функции в точке.

3. Неперывность основных элементарных функций.

4. Свойства функций, непрерывных в точке.

5. Точки разрыва функции, их классификация.

6. Свойства функций, непрерывных на отрезке.

7. Заключение.

1. Введение

Понятие непрерывности мы интуитивно связываем с представлением о непрерывной “сплошной” линии, какую описывает, например, непрерывно движущийся кусок мела на доске. Дадим понятию непрерывности строгое определение. В дальнейшем, опираясь на это определение, изучим свойства непрерывных функций. Изучение более широких классов функций удается свести к изучению непрерывных функций.

Установление понятия непрерывности в точной форме принадлежит чешскому физику и математику Б.Больцано (1781-1848г.г.) и французскому математику О.Коши (1789-1857г.г.).

2. Определение непрерывности функции в точке.

Определение 1. Функция f(x) , определенная в точке x₀ и некоторой ее окрестности, называется непрерывной в точке x₀ , если предел функции при xx₀ равен значению функции в точке x₀

.

Итак, чтобы функция f(x) , была непрерывна в точке x₀ , необходимо и достаточно, чтобы:

1. функция f(x) была определена в самой точке x₀ и в некоторой ее окрестности;

2. в точке x_o функция f(x) должна иметь конечный предел;

3. этот предел должен быть равен значению функцию в точке x₀ .

Пример. Пользуясь определением, покажем непрерывность функции f(x)=5x+10 в точке x₀= -1.

1. f(x)=5x+10 определена всюду на ( , следовательно, и вточке x₀= 1.

2.

( Предел находим, пользуясь теоремами о пределе суммы, постоянного и вынесения постоянного множителя за знак прердела).

3. f(-1)=5(-1)+10=5.

Итак,

Используя определение предела на “языке “, можно дать второе определение непрерывности функции в точке.

Определение 2. Функция f(x) называется непрерывной в точке x₀ , если для любого числа  найдется такое число  , что для всех значений x , удовлетворяющих условию x-x₀< выполняется неравенство f(x)-f(x₀) .

Покажем, что данные определения непрерывности соответствуют наглядному представлению о непрерывности графика функции.

По определению предела

Причем, теперь x при стремлении к x₀ принимает значение x₀ . Поэтому не вводится оговорка xx₀ .

x-x₀<x₀ <x<x₀+

f(x)-f(x₀)<f(x₀)-<f(x)<f(x₀)+ .

Геометрически это значит, что для любой полосы плоскости, ограниченной прямыми y=f(x₀)- и y=f(x₀)+ существует интервал x₀-<x<x₀+ такой, что соответствующие ему точки графика y=f(x) целиком лежат в этой полосе плоскости (рис.1).

Рис.1

Так как полоса, ограниченная прямыми y=f(x₀)- и y=f(x₀)+ может быть выбрана как угодно узкой, то точки графика y=f(x) как угодно близки к точке (x₀ , f(x₀)), если только их абсциссы достаточно мало отличаются от числа x₀. Именно это и создает то зрительное впечатление, которое выражается словами “ сплошная линия ”, “ непрерывная линия ”.

На рис.2 изображен график функции, не являющейся непрерывной в точке x₀.

Рис.2

Используя определение предела “ на языке последовательностей ”, можно дать

Определение 3. Функция f(x) называется непрерывной в точке x₀, если для любой последовательности значений аргумента x_n, сходящейся к x₀, соответствующая последовательность значений функции f(x_n) сходится к f(x₀).

Определение 4. Функция f(x) называется непрерывной справа (слева) в точке x₀, если предел функции справа (слева) при xx₀ равен значению функции в этой точке:

f(x₀+0)=f(x₀) (рис.3) или f(x₀ - 0)=f(x₀) (рис.4)

Рис.3

Рис.4

Если функция f(x) непрерывна в точке x₀, то она непрерывна слева и справа в этой точке, т.е. определение непрерывности можно записать

f(x₀ - 0)=f(x₀)=f(x₀+0).

Если функция непрерывна в точке x₀ , то

т.е. для функции, непрерывной в точке, знаки функции и предела можно менять местами. Чтобы найти предел непрерывной функции, надо в выражение функции вместо аргумента подставить его предельное значение.

Данные определения непрерывности удобны для установления непрерывности функции в точке. Рассмотрим определение, которое можно использовать при установлении непрерывности функции на множестве значений аргумента.

Определение 5. Функция f(x) называется непрерывной в точке, если бесконечно малое приращение аргумента вызывает бесконечно малое приращение функции.

Пусть дана функция y=f(x). Предлоложим, что от значения x₀ мы перешли к значению x. Обозначим x=x-x₀ , y=f(x)-f(x₀). x - приращение аргумента, y - приращение функции. Знак приращения может быть любой. Предположим, что функция y=f(x) непрерывна в точке x₀ . По определению 1

3. Непрерывность основных элементарных функций

Используя определение 5, нетрудно доказать непрерывность основных элементарных функций в области их определения.

Докажем непрерывность функции y=sinx в точке x(-).

Запишем приращение функции

Но . Тогда

Аналогично доказывается непрерывность основных элементарных функций cos x , tg x , ctg x , xⁿ , a^x .

Если функция y=f(x) непрерывна и имеет обратную функцию x=(y), то последняя также непрерывна. Интуитивно это понятно, т.к. графиками функций y=f(x) и x=(y) является одна и та же линия.

На основании этого непрерывны функции arcsin x, arccos x, arctg x, arcctg x, log_a x.

4. Свойства функций, непрерывных в точке

1. Сумма, разность, произведение конечного числа функций, непрерывных в точке, непрерывны в этой точке.

Доказывается на основании теорем о пределах.

2. Частное от деления двух функций , непрерывных в точке x₀ , непрерывно в этой точке, если (x₀)0.

Доказательство.

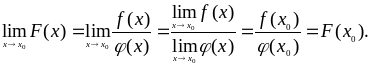
3. Если u=(x) непрерывная функция в точке x₀ : u₀=(x₀), а функция y=f(u) непрерывна в точке u₀ , то сложная функция y=f[(x)] непрерывна в точке x₀ .

Т.о., суперпозиция непрерывных функций есть непрерывная функция. Следовательно, всякая элементарная функция непрерывна во всех точках, принадлежащих области ее определения.

5. Точки разрыва функции, их классификация

Если хотя бы одно из условий непрерывности в точке x₀ не выполняется :

1. функция не определена в точке x₀ ;

2. функция не имеет в точке x₀ конечного предела ;

3. предел функции в точке x₀ не равен значению функцции в этой точке,

точка x₀ называется точкой разрыва.

Различают точки разрыва первого и второго рода.

Определение. Точка разрыва называется точкой разрыва 1 рода, если в этой точке функция имеет конечные пределы справа и слева.

Таким образом, если x₀ - точка разрыва 1 рода функции f(x), то график этой функции в точке x₀ может иметь лишь конечный скачок.

Определение. Точка разрыва называется точкой разрыва 2 рода, если в этой точке функция не имеет по крайней мере одного из односторонних пределов (конечного).

Пример 1.

График функции изображен на рис.5

Рис.5

Функция не определена в точке x=0. Здесь x=0 является точкой разрыва 1 рода. Если доопределить f(x) в точке x=0, положив f(0)=0, то

будет иметь разрыв 1 рода .

Если доопределить f(x) в точке x=0, положив f(0)=1, то f(x) имеет разрыв 1 рода , но она будет непрерывна в точке x=0 справа.

Аналогично, если f(0)=1, то функция непрерывна слева.

Пример 2. (рис.6)

Рис.6

В точке x=0 функция не определена, но она имеет конечные пределы слева и справа в этой точке

Следовательно, при x=0 функция имеет разрыв 1 рода.

Если доопределить функцию, положив f(0)=1, то функция 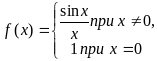будет непрерывна в точке x=0, т.е. разрыв устраняется. Случай устранимого разрыва есть частный случай разрыва 1 рода.

Пример 3. x=0 - точка разрыва 2 рода: f(+0)=+ , f(-0)=0. График этой функции изображен на рис.7.

Рис.7

Пример 4. f(x)=sin (рис.8)

Рис.8

Как было показано, эта функция не имеет предела при x0, следовательно, в точке x=0 она имеет разрыв 2 рода.

Пример 5. Функция Дирихле: f(x)=0 для всех иррациональных значений x и f(x)=1 для всех рациональных значений x, разрывна в каждой точке; точки разрыва 2 рода.