4. Основные теоремы о пределах.
Теорема 1. Если
функция f (x)
имеет предел
,
то ее можно представить как сумму этого
предела и бесконечно малой функции
(x)
при x a:
f (x) = A + (x)
Доказательство.
По определению предела |f (x) – A| < при
< |x – a| < .
Обозначим f (x) – A = (x). |f (x) – A| = |(x)|.
Тогда |(x)| < при |x – a| < т.е. (x) - бесконечно малая при x a.
Теорема
2 (обратная).
Если функцию можно представить как
сумму постоянного числа
и бесконечно малой функции при x a,
то постоянное слагаемое является
пределом этой функции при x a.
Теорема 3. Функция не может иметь более одного предела.
Доказательство. Предположим противное. Пусть lim f (x) = A, lim f (x) = B и A B. Тогда f (x) = A + (x) и f (x)= B + (x), где (x) и (x) бесконечно малые функции при x a.
Вычтем почленно
из первого равенства второе
0 = (A – B) + ( (x) – (x))
или B ‑ A = (x) ‑ (x).
Но (x) – (x) -
бесконечно малая функция при x a,
т.е.
.
Следовательно: B – A = 0 B = A.
Теорема 4. Предел алгебраической суммы функций, имеющих пределы, равен алгебраической сумме пределов.
Доказательство.
при xa
при xa.
Тогда
.
Замечание. Теорема справедлива для алгебраической суммы любого конечного числа слагаемых.
Теорема 5. Предел произведения любого конечного числа функций, имеющих пределы, равен произведению их пределов.
Доказательство. при x a
.
Следствие. Постоянный множитель можно выносить за знак предела.
Замечание. Предел постоянной есть сама постоянная.
.
Следовательно ,
Теорема 6. Предел частного двух функции, каждая из которых имеет предел, равен частному пределов этих функций, если предел знаменателя не равен нулю.
Доказательство. Рассмотрим разность
Она является бесконечной молой при xa . Следовательно , теорема доказана.
Пример.
Замечание . При
практическом вычислении пределов с
использованием теорем 4-6 могут получиться
неопределенности вида (
)
, ( 0
), (
)
или (
).
В этих случаях путем различных
преобразований функцию, стоящую под
знаком предела приводят к виду, когда
можно применять рассмотренные теоремы.
Вычисление пределов в этих случаях
называется раскрытием неопределённостей.
Примеры.
1.
2.
3.
ЛЕКЦИЯ №
БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
План
1. Введение.
2. Некоторые пределы.
3. Бесконечно большие функции и их связь с бесконечно малыми.
4. Сравнение бесконечно малых функций.
5. Свойства эквивалентных бесконечно малых.
6. Заключение.
I.Введение
Рассмотрим вычисление некоторых важных для практических приложений примеров вычисления пределов функций.
2.Некоторые пределы
I.Предел отношения
при x
0.
называют первым
замечательным пределом. Найдем этот
предел. Непосредственное применение
теоремы о пределе частного дает
неопределенность вида
.
Рассмотрим функцию
(x)
=
,
которая определена всюду, кроме точки
ноль. Эта функция четная, т.к. (-x)
=
=
(x).
По условию x
0, следовательном можно рассмотреть
значения x
, удовлетворяющие неравенствам 0 < x
<
.
|
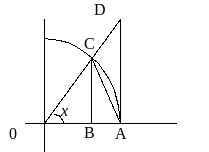
пл. ОАС < пл. сектора ОАС < пл. OAD (Рис. 1) пл.
ОАС =
пл.
сектора ОАС =
ОА
пл. ОАD = ОА АD = R2 tg x |
ОА
ВС =
R2
sin x;
=
R2x
Рис.1
Откуда sin x < x < tg x
Так как sin x
> 0, то разделив эти неравенства на sin
x,
получим 1 <
<
или
cos x
= 1 ,следовательно
Формула справедлива
и в случае
,так
как функция
четная.
Примеры.
I.
.
2.
.
3.
.
.
2.
-
второй замечательный предел.
=
e.
Пусть x>0 , тогда
,
где
—
натуральное число , а
удовлетворяет
условию 0
.
При x
.
.
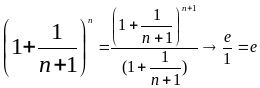Тогда
Аналогичным образом
,если x<-1.
x=-y,
x-
y+
.
Вторая форма записи
второго замечательного предела
Пример.
3. Бесконечно большие функции и их связь с бесконечно малыми.
Функция
называется бесконечно большой при xa
, если для любого числа
существует число
, такое , что неравенство f(x)M
выполняется для всех x
, удовлетворяющих условию x-a
.
Обозначают:
или
Спомощью кванторов определение бесконечно большой функции можно записать
Графики таких функций изоборажены на рис.2-4
Рис.2
Рис.3
Рис.4
Связь между бесконечно большими и малыми при xa функциями устанавлевается теоремой.
Теорема. Если
функция f(x)
- бесконечно
малая при xa
и f(x)0
вблизи a,
то функция
- бесконечно большая при xa
и наоборот.
Доказательство. По определению бесконечно большой функции
4. Сравнение бесконечно малых функций.
Пусть
- функции бесконечно малые при xa
(a-число,
+,
- ).
Бесконечно малые
функции сравнивают между собой по
быстроте стремления к нулю. Если
, то (x)
называется бесконечно малой более
высокого порядка, чем (x)
.
Условно это записывают так: 0
или x)=0((x)).
Замечание. Символ “O” используется при сравнении двух функций.
Если для функций f(x) и (x) существует такое число с>0 , что |f(x)|<c|(x)| при xa (xa) , то говорят что f(x) является ограниченной по сравнению с функцией (x) в некоторой окрестности точки x=a и обозначают f(x)=O((x)).
Пример.
при x0.
Если
существует и отличен от нуля, то (x)
и (x)
называются
бесконечно малыми одного порядка. В
частном случае, когда этот предел равен
1, бесконечно малые (x)
и (x)
называются
эквивалентами бесконечно малыми при
xa
. Обозначают (x)(x).
Пример. (x)=sin
x; (x)=x.
т.к.
.
Бесконечно малая
(x)
называется бесконечно малой порядка k
относительно
бесконечной малой (x)
, если
конечен и отличен от нуля.
Пример.
(x)= x sin x; =x.
.
- бесконечно малая второго порядка относительно .
Бесконечно малые
(x)
и (x)
называются
несравнимыми, если
не существует.
Пример (x)=x
sin
;
(x)=x
- несравнимы.
5. Свойства эквивалентных бесконечно малых
1.
. (
).
2. Если
то
.
3. Если
и
, то
.
На этом свойстве построена таблица эквивалентных бесконечно малых. Особенно важное свойство для практических приложений, в частности, для вычисления пределов.
4. Если 1
, 1
и
, то
, т.е. предел отношения бесконечно малых
не меняется при замене их эквивалентными
бесконечно малыми, т.е.
Пример.
при x tg5x5x , sin7x7x.
Замечание. Некоторые наиболее важные эквивалентные бесконечно малые при x0 :
x sin x tg x arcsin x arctg x ln(1+x) ex-1.
Если
, то
sin f(x)
tg f(x)
arcsin f(x)
arctg f(x)
ln(1+f(x))
ef(x)-1.
Пример.
x3 , sin (x-3) x-3.