6. Число e.

Рассмотрим последовательность с общим членом . Покажем, что она имеет предел. Формула бинома Ньютона:

По формуле бинома Ньютона ;

;

;

;

.

Тогда

1. С ростом n каждое слагаемое и их число увеличивается. Следовательно, последовательность {x_n}монотонно возрастает.

2. Покажем, что последовательность ограничена:

;

.

,

т.е. последовательность ограничена и, следовательно, она имеет предел

,

e = 2,71828 иррациональное число.

Логарифмы чисел по основанию е называют натуральными логарифмами и обозначают log_ex = ln x.

Связь между натуральными и десятичными логарифмами

y = ln х, х = е^y lg х = lg e^y = y lg e lg х = ln х  lg e.

lg е = 0,4343

7. Заключение.

Жизнь (физика, механика, техника) ставит перед математикой определенные задачи. Математика дает методы их решения в обобщенной и абстрактной форме. Практика использует эти методы для всевозможных расчетов. Только для философа-идеалиста математика - это произвольное и свободное творение человеческого ума, никак не обусловленное задачами естествознания и техники.

Ф.Энгельс по поводу абстрактности математики писал “Как понятие числа, так и понятие фигуры заимствованы исключительно из внешнего мира, а не возникли в голове из чистого мышления. Должны были существовать вещи, имеющие определенную форму, и эти формы должны были подвергаться сравнению, прежде чем можно было прийти к понятию фигуры Но чтобы быть в состоянии исследовать эти формы и отношения в чистом виде, необходимо совершенно отделить их от их содержания, оставить это последнее в стороне как нечто безразличное таким путем мы получаем точки, лишенные измерений, линии, лишенные толщины и ширины, разные а и b, х и у, постоянные и переменные величины”.

ЛЕКЦИЯ №

Предел функции

1. Введение.

2. Определение предела функции.

2.1. Геометрический смысл определения предела функции в точке.

3. Ограниченность функции, имеющей предел.

4. Свойства пределов функций, связанные с неравенствами.

5. Заключение.

Операция предельного перехода играет важную роль в математическом анализе. Впервые определение понятия предела появляется у Дж.Валлиса (1616-1703). (“Арифметика бесконечных”, 1665 г., Валлис был членом -учредителем королевского общества, профессором геометрии в Оксфорде). Однако только в работах О.Коши (1789-1857) и Б.Больцано (1781-1848 г.)была впервые развита теория пределов и использована для строгого построения всего математического анализа. Коши и Больцано принадлежат к пионерам в деле внедрения в математику повышенной строгости. Коши дал то обоснование анализа, которое сейчас является общепринятым в наших учебниках. Коши использовал понятие предела, чтобы определить производную от функции, таким образом, более прочно обосновал это понятие, чем были в состоянии сделать его предшественники.

Все окружающие нас задачи имеют дело с переменными величинами. Эти задачи в основном связаны с необходимостью уметь подсчитывать пределы переменных величин, приращения переменных величин, отношения этих приращений, когда они бесконечно малы, и пределы сумм бесконечно малых. Поэтому изучают бесконечно малые не случайно, а по тому, что их использование носит всеобщий характер. Все явления природы в конечном счете имеют своим источником движение материи. Но с движущейся частицей связаны понятия: траектория, время, скорость и ускорение. Измерение величины движущейся массы связано с понятиями плотности, длины дуги, площади и объема. Таким образом, во всех основных расчетах в науке и технике мы подсчитываем либо пределы отношений бесконечно малых (скорость, ускорение, плотность), либо пределы сумм бесконечно малых (длина дуги, площадь, объем, масса). Следовательно, эти операции анализа являются важнейшими вычислительными операциями науки и техники.

1. Определение предела функции.

Пусть функция f(x) определена в некоторой окрестности точки . В точке функция может быть и не определена.

Определение 1. Число A называется пределом функции f(x) при х стремящемся к , если для любого положительного числа (  0) найдется такое положительное число  (  ), что для всех x, удовлетворяющих условию x –    , выполняется неравенство fx    .

Это определение с помощью кванторов можно записать так:

Пример. Пользуясь определением предела, покажем, что

f(x) = 4x + 7, A = 11, a = 1.

По определению предела

           x    x      

Пусть . Найдем  такое, чтобы для

.

Но . Следовательно .

Для любого >0 найдем  такое, что

,

следовательно .

1.1. Геометрический смысл определения предела функции в точке

Рассмотрим функцию y = f(x), график которой представлен на рис.1. В точке x=a функция может быть не определена. Построим произвольно - окрестность точки A. Проведем прямые y = A –  и y = A + . Справа и слева от точки a на оси OX получим отрезки. Меньший из них примем за  и построим  - окрестность точки a.

Рис.1

Из определения предела функции следует, что для любого    ( может быть сколь угодно малым) существует  > 0, такое, что для всех точек симметричного относительно a интервала (a  , a   ) значения функции не входят из  - окрестности точки a.  зависит от    ).

Из рассмотрения графиков функций, изображенных на рис.2 и 3 ясно, что эти функции не имеют предела при x  a.

Рис.2	Рис.3

Определение 2. Число A называется пределом функции f(x) при x  a, если для любой последовательности значений аргумента x: x₁, x₂, , x_n, …, сходящейся к a, соответствующая последовательность значений функции f(x₁), f(x₂) …, f(x_n), … сходится к A.

Это определение с помощью кванторов можно записать так:

.

Определение 1 называют ( – ) - определением предела, а определение 2 - определением предела “на языке последовательностей”. Определения 1 и 2 эквивалентны.

Определение предела функции через предел последовательности дает возможность из теорем, полученных для сходящихся последовательностей, получить соответствующие теоремы о пределах функций. Оно дает также возможность установить для некоторых функций, что они не имеют предела. Для этого достаточно показать, что существует последовательность значений аргумента сходящаяся к рассматриваемому значению аргумента, для которой соответствующая последовательность значений функции не имеет предела, или показать, что существуют две различные последовательности, сходящиеся к рассматриваемому значению аргумента, для которых соответствующие последовательности значений функции имеют различные пределы.

Пример: Функция не имеет предела при x  0.

; ; (x^/_n) = sin n = 0  0.

; ; .

В некоторых случаях возникает необходимость исследовать поведение функции, когда аргумент неограниченно растет по абсолютной величине. Может оказаться, что значения функции при этом стремятся к некоторому числу . Определим предел функции при стремлении аргумента к бесконечности.

Определение 3. Число  называется пределом функции (x) при x  , если для любого   0 найдется такое число   0, что для вех значений x, удовлетворяющих неравенству |x|  , выполняется неравенство | (x)  |  , или

.

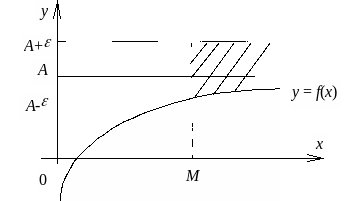
Если , то график функции (x) неограниченно (асимптотически) приближается к прямой y =  при стремлении x к  как по положительным, так и по отрицательным значениям (рис.4).

Рис.4

Аналогично определяются пределы

, (рис.5)

, (рис.6)

Рис.5	Рис.6