4. Предел последовательности.
Определение. Числа a называется пределом последовательности {xn}, если для любого положительного числа > 0 найдется такой номер N, что для всех n > N выполняется неравенство |a – xn| < .
Если последовательность
имеет предел, то это записывают
и говорят, что последовательность {xn}
сходится (сходится к a),
или имеет конечный предел.
Определение предела последовательности с помощью кванторов можно записать так:
xn = а 0 :
n
|a xn|
Замечание. может быть любым положительным числом, в частности, сколь угодно малым.
Пример 1. Найти предел последовательности:
0,3; 0,33; 0,333; 0,3333; …
Проверим, будет ли 0,4 являться пределом последовательности. Рассмотрим разности
|0,4 – 0,3| = 0,1; |0,4 – 0,33| = 0,07; |0,4 – 0,333| = 0,067; |0,4 – 0,3333| = 0,0667; …
Абсолютная величина разности всегда больше 0,06. Поэтому 0,4 не является пределом последовательности.
Проверим, будет
ли
пределом последовательности.
;
;
;
;
Абсолютная величина
разности уменьшается неограниченно,
становясь меньше любого как угодно
малого числа. Следовательно
Пример 2. Пользуясь определением предела последовательности доказать
Пусть
;
неравенство
справедливо при n
5. Следовательно, за N
можно принять 5.
Пусть
= 0,01; неравенство
справедливо при n
99. Следовательно, N
= 99.
Для любого
0 неравенство
справедливо при
.
Следовательно, за N
можно взять целую часть числа
.
Номер N зависит от величины : N = N().
4.1. Геометрическая интерпретация определения предела последовательности.
На числовой прямой число а изображается точкой. Произвольно выбрав 0, построим - окрестность точки а.
Рис.6
Если последовательность {xn} имеет пределом число а, то члены последовательности при всех n > N (n ) удовлетворяют неравенствам а < xn < а , т.е. все члены последовательности, начиная с некоторого, будут изображаться точками, лежащими в - окрестности точки а.
Если это условие не выполняется, число а не является пределом последовательности. В качестве N условимся брать номер члена, оказавшегося на границе окрестности, или номер члена, оказавшегося перед границей, если на границе члена нет.
Пример. Покажем,
что число 0 является пределом
последовательности
,
т.е.
.
или
.
За
выберем
.
Построим - окрестность
точки O.
Р
ис.7
Все члены последовательности, номера которых больше трех, попадут в эту окрестность. Следовательно, за N можно взять 3.
Пусть
,
тогда N =
5, т.к. все члены последовательности,
номера которых больше 5, попадут в -
окрестность точки 0.
Т.о., если откладывать точки, изображающие члены последовательности на числовой оси, то они будут как бы накапливаться в точке а.
Если члены последовательности изображать графиком в декартовой системе координат (по оси абсцисс значения n, по оси ординат значения членов {xn}), то все точки, лежащие правее прямой n = N, окажутся внутри полосы шириной 2 (рис.7)
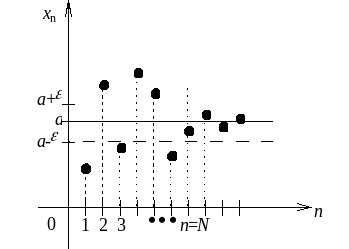
Рис.7
Из определения предела следует, что две последовательности, отличающиеся между собой на конечное число членов, ведут себя одинаково относительно сходимости.