3. Числовые последовательности.

Пусть каждому натуральному числу n поставлено в соответствие число x_n. Тогда говорят, что задана последовательность x₁, x₂, … , x_n, … или {x_n}.

Определение. Функция, областью определения которой является множество натуральных чисел, называется числовой последовательностью.

Пример 1. a_n – величина внутреннего угла правильного многоугольника; n - число стосторон многоугольника.

n: 3, 4, 5, …, n, …

Пример 2. s_n - величина площади квадрата со стороной в n единиц длины.

n: 1, 2, 3, …, n, …

s_n: 1, 4, 9, …, n², …

Общий член последовательности {x_n} является функцией натурального аргумента n: x_n = fn).

Давая различные значения n = 1, 2, 3, …, получим последовательность значений этой функции (члены последовательности):

f(1), f(2), …, f(n), …

Функция f(n) может быть задана любым способом: аналитически, таблицей, графически и т.д.

Примеры:

1. или

2.	если n нечетное, если n четное.

или .

Геометрическое изображение последовательности.

1 способ - построение графика функции (n).

Рассмотрим последовательность или

Рис.1

График функции (n) представляет собой последовательность изолированных друг от друга точек на плоскости (pис.1.)

2 способ - изображение последовательности точками числовой прямой.

Построив на числовой оси точки с абсциссами, равными величинам соответствующих членов последовательности {x_n}, получим последовательность точек, которая является геометрическим изображением данной последовательности.

На рис.2 изображена последовательность .

Рис.2

Последовательность {x_n} называется ограниченной, если существует число М  0, такое, что для всех n выполняется неравенство |x_n|  M. Геометрически это означает, что все члены последовательности принадлежат интервалу –M, M ) (рис.3)

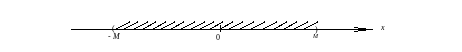
Рис.3

Замечание. Число M не обязательно наименьшее, удовлетворяющее этому условию.

Пример. - ограниченная последовательность, т. к. .

Последовательность, не являющаяся ограниченной , называется неограниченной. Для неограниченной последовательности при любом М > 0 найдутся члены последовательности, которые лежат вне интервала (–М, М). Например: {n}; {n!}.

Последовательность {x_n} называется ограниченной сверху (справа), если все ее члены меньше некоторого числа М, т.е. x_n < М. Все члены последовательности принадлежат интервалу (–, М) (рис. 4).

Рис.4

Рис.5

Число М называется верхней гранью последовательности {x_n}.

Последовательность ограничена снизу (слева), если существует число m, такое, что неравенство x_n > m выполняется при всех n, т.е. члены последовательности принадлежат интервалу (m, ) (рис. 5).

Число m называется нижней гранью последовательности {x_n}.

Из определений следует, что если последовательность ограничена, то она ограничена и сверху и снизу.

Замечание. Любая ограниченная сверху (снизу) последовательность имеет бесчисленное множество верхних (нижних) граней.

Примеры:

1) {n} - ограничена снизу;

2) {–n} - ограничена сверху;

3) - ограниченная |x_n| < 2.