6. Свойства функций, непрерывных на отрезке
Определение. Функция f(x) называется непрерывной на интервале (a,b), если она непрерывна в каждой точке этого интервала.
Определение. Функция f(x) называется непрерывной на отрезке a,b, если она непрерывна на интервале (a,b) и, кроме того, непрерывна справа в точке a и слева в точке b.
Рассмотрим основные свойства функции, непрерывной на отрезке. Эти свойства будем рассматривать без доказательства. Поэтому дадим лишь формулировки теорем и их геометрическую иллюстрацию.
1. Функция, непрерывная на отрезке, огранича на этом отрезке.
Это означает, что существует число M>0, такое, что для всех точек отрезка a,b выполняется неравенство f(x)<M.
Геометрически: график функции f(x) на рассматриваемом отрезке не выходит из полосы M<y<M (рис.9).
Рис.9
Доказательство этого утверждения основывается на том, что функция, непрерывная в точке x0, ограничена в некоторой ее окрестности.
Замечание. Это
утверждение перестает быть верным, если
функция непрерывна на интервале или
полуинтервале. Например,
непрерывна (0,1), но не является ограниченной
на этом интервале.
2. Функция f(x), непрерывная на отрезке a,b, принимает на этом отрезке наибольшее и наименьшее значения, т.е. существуют такие точки x1 и x2 отрезка a,b, что f(x1)=m , f(x2)=M и для всех точек отрезка mf(x)M (рис.10).
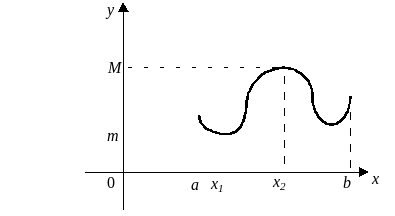
Рис.10
Наибольшее и наименьшее значения функция может принимать несколько раз (например, sin x).
3. Функция f(x) непрерывная на отрезке a,b, принимает на этом отрезке все значения между любыми двумя ее значениями.
Геометрически это очевидно. f(x1)=A , f(x2)=B.
Пусть C - любое: A<C<B. Тогда прямая y=C пересечет график функции по крайней мере в одной точке (рис.11).
Рис.11
4. Если функция f(x) непрерывна на a,b и на его концах принимает значения разных знаков, то внутри этого отрезка найдется по крайней мере одна точка, в которой функция обращается в ноль.
Точка, в которой функция обращается в ноль, может быть не единственной. На рис.12 таких точек три: x1 , x2 , x3 .
Рис.12
Это свойство лежит в основе отыскания корня уравнения f(x)=0 методом половинного деления.
7. Заключение
Таким образом, рассмотрено определение непрерывности функции в точке и на промежутке, базирующееся на определении предела функции. Определены точки разрыва функции и установленна их классификация. Рассмотрены свойства функций, непрерывных в точке и на отрезке. Понятие непрерывности функции является одним из важнейших понятий математического анализа. Оно отражает свойства реального мира.