Тестові завдання з математики (1 курс)

Тема 1. Елементи лінійної та векторної алгебри

1. Добутком матриці А (m x n) на матрицю В (n x p) називається матриця С (m x p), кожен елемент C_ij якої дорівнює:

2. Квадратна матриця, визначник якої дорівнює нулю, називається

3. Систему m лінійних алгебраїчних рівнянь з n невідомими розв’язують матричним методом, якщо

4. Система лінійних алгебраїчних рівнянь, що має хоча б один розв’язок, називається

5. Базисом на площині називають

6. Задано вектори (…) та (…). Знайти скалярний добуток векторів .

7. Модуль мішаного добутку трьох не компланарних векторів, які віднесені до спільного початку, дорівнює

8. Маємо добуток чотирьох матриць А(3 х 2), В(2 х 4), С(4 х 1), Д(1 х 5). Який розмір буде мати кінцева матриця ?

9. У визначнику третього порядку третій рядок помножили на два і додали до першого. Як в цьому випадку змінилась величина визначника ?

10. Скільки розв’язків має система лінійних алгебраїчних рівнянь, якщо rang B > rang A, де А – основна матриця системи, а В – розширена матриця.

11. Визначник матриці однорідної системи n лінійних рівнянь з n невідомими не дорівнює нулю. Скільки розв’язків буде мати ця система ?

12. Вектори а₁, а₂, а₃ називаються лінійно незалежними, якщо їх лінійна комбінація α а₁ + 𝛽 а₂ + γ а₃ дорівнює нулю лише при виконанні умови:

13. Знайти вектор , колінеарний до вектора (…).

14. Два вектори а і в колінеарні тоді і тільки тоді, якщо

15. Матриця А називається узгодженою з матрицею В, якщо

16. У визначнику третього порядку елементи двох стовпців пропорційні. Чому дорівнює величина визначника ?

17. Матриця А^-1 називається оберненої до матриці А, якщо виконується умова

18.Система лінійних алгебраїчних рівнянь називається однорідною, якщо

19. Ранг матриці А rang (A) = 0, якщо

20. Базисом у просторі називають

21. Знайти довжину вектора , якщо А (…), В (…).

22. Висоту трикутної піраміди, яка побудована на векторах можна обчислити за формулою:

Тема 2. Аналітична геометрія

23. Який висновок можна зробити про розміщення двох прямих?

24. Кутом φ нахилу прямої називається

25. Задано площину … та пряму … Як розміщені пряма та площина?

26. Який висновок можна зробити про розміщення площини …?

27. Знайти координати напрямного вектора прямої

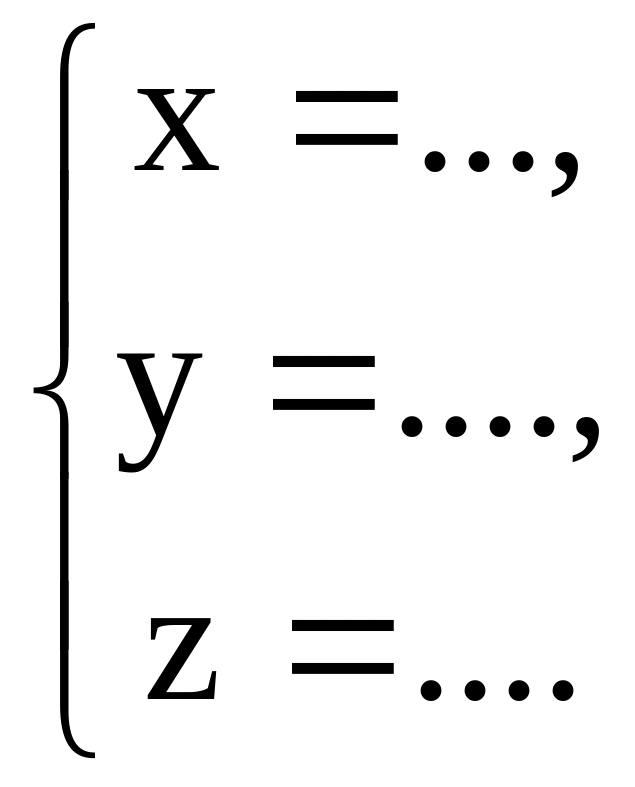
28. Знайти центр кола, діаметром якого є відрізок ОD, якщо О( …), D (…).

29. Довжина дійсної півосі гіперболи a = …, а уявної півосі b = …. Знайти відстань між фокусами.

30. По якої лінії перетинається конус … з площиною …?

31. Знайти площу прямокутного трикутника, що утворює пряма … з осями координат.

32. Пряма має кутовий коефіцієнт к₁ = …. Який кутовий коефіцієнт к₂ буде мати пряма, яка перпендикулярна до неї ?

33. Знайти рівняння прямої, кут нахилу який дорівнює …º і яка відсікає на додатному напряму осі ординат відрізок в = ….

34. Знайти відстань від точки М (…) до прямій … .

35. Який висновок можна зробити про розміщення площини ….

36. Знайти модуль нормального вектора площини ….

37. Довжина великої півосі еліпса дорівнює …, а малої півосі дорівнює …. Знайти відстань між фокусами.

38. Яку поверхню визначає в просторі рівняння … ?

39. Знайти кут нахилу прямої у = … .

40. Знайти координати напрямного вектора прямої … .

41. Знайти модуль нормального вектора прямої … .

42. Що можна сказати о взаємному розташуванні площин … та … ?

43. Для гіперболи відомо, що

44. Для параболи … знайти рівняння її директриси.

45. По якої лінії площина … перетинає одно порожнинний гіперболоїд …?