
- •Элементы комбинаторики (размещения, перестановки, сочетания)
- •2. Событие. Виды случайных событий.
- •3. Классическое и статистическое определение вероятностей. Св-ва.
- •4. Теорема сложения вероятностей несовместных событий.
- •5. Зависимые и независимые события. Условная вероятность.
- •6. Теорема умножения вероятностей зависимых и независимых событий.
- •7. Формула полной вероятности.
- •8. Формула Байеса.
- •9. Понятие случайной величины (св). Закон распределения дискретной случайной величины (дсв).
- •10. Функция распределения (фр) и ее св-ва.
- •11. Плотность распределения и ее св-ва.
- •12. Математическое ожидание и дисперсия дсв. Св-ва.
- •13. Числовые характеристики непрерывных св.
- •14. Формула Бернулли.
- •19. Закон распределения Пуассона
- •29. Оценка ген. Средней по выборочной средней
- •30. Ошибка выборки при определении ср значения признака выборки
- •31. Стат. Оценка параметров. Смещенные и несмещенные оценки
- •32. Формулы доверительных вероятностей. Доверит границы для ген средней и ген доли.
- •34. Необходимый объем выборки
- •39. Статистическая гипотеза. Нулевая и конкурирующая гипотезы.
- •40. Уровень значимости и мощность критерия.
- •35.Функцион. И стат. Зависимости. Корреляционная таблица
- •36. Условные средние. Корреляционная зависимость
- •37. Уравнение прямых регрессий
- •41. Проверка гипотезы о среднем значении при известной и неизвестной дисперсиях.
- •42. Проверка гипотезы о рав-ве значений 2ух средних из нормально распределенных ген совокупностей.
- •43. Критерий согласия Пирсона.
- •5. Зависимые и независимые события. Условная вероятность.
- •11. Плотность распределения и ее св-ва.
- •28. Понятие о выборочном методе. Хар-ки ген и выбор совокупности
37. Уравнение прямых регрессий
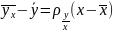 – уравнение
прямой регрессии у/х,
где коэффициент регрессии вычисляется
по формуле:
– уравнение
прямой регрессии у/х,
где коэффициент регрессии вычисляется
по формуле:
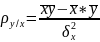 .
Аналогично получаем ур-е
прямой регрессии по х/у:
.
Обе
прямые регрессии проходят через точку
(
.
Аналогично получаем ур-е
прямой регрессии по х/у:
.
Обе
прямые регрессии проходят через точку
(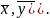
41. Проверка гипотезы о среднем значении при известной и неизвестной дисперсиях.
Для
проверки гипотезы о значении генеральной
средней на основании результатов
выборки объема n
при известной ген дисперсии
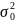 для нормального распределения признака
X,
необходимо проверить гипотезу
для нормального распределения признака
X,
необходимо проверить гипотезу
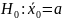 ,
те проверить предположение о рав-ве
ген среднего значения
,
те проверить предположение о рав-ве
ген среднего значения
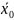 со значением a,
при альтернативной гипотезе
со значением a,
при альтернативной гипотезе
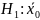 =
=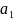 (
(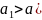 .
В кач-ве стат критерия возьмем нормально
распред СВ Z=
.
В кач-ве стат критерия возьмем нормально
распред СВ Z=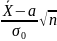 ,
где
,
где
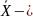 среднее
выборки, n
– объем выборки. Для Z
ф-я распределения: F(Z)=0,5(1+Ф(Z)).
Критическая область определяется
неравенством |z|≥|
среднее
выборки, n
– объем выборки. Для Z
ф-я распределения: F(Z)=0,5(1+Ф(Z)).
Критическая область определяется
неравенством |z|≥|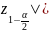 .
Рассмотрим случай, когда распределение
признака X
подчинено нормальному з-ну распределения
с неизвестной дисперсией
.
Осуществим проверку гипотезы
при альтернативной гипотезе
=
(
.
В этом случае в кач-ве статистики
критерия возьмем СВ T=
.
Рассмотрим случай, когда распределение
признака X
подчинено нормальному з-ну распределения
с неизвестной дисперсией
.
Осуществим проверку гипотезы
при альтернативной гипотезе
=
(
.
В этом случае в кач-ве статистики
критерия возьмем СВ T=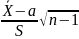 , где
, где
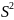 - статистическая дисперсия,
среднее
выборки. Критическая область определяется
неравенством |T|≥
- статистическая дисперсия,
среднее
выборки. Критическая область определяется
неравенством |T|≥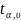 ,
где величину
,
где величину
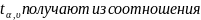 P=(|T|≥
)=α.
P=(|T|≥
)=α.
42. Проверка гипотезы о рав-ве значений 2ух средних из нормально распределенных ген совокупностей.
Проверим
гипотезу
о рав-ве средних нормально распределенных
СВ X
и Y
(
:
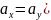 .
Альтернативная гипотеза
:
.
Альтернативная гипотеза
:
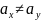 .
Рассмотрим случай, когда дисперсия
.
Рассмотрим случай, когда дисперсия
 и
и
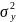 известны. Тогда для проверки гипотезы
воспользуемся законом распределения
разности средних
известны. Тогда для проверки гипотезы
воспользуемся законом распределения
разности средних
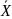 и
и
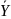 .
Заметим, что
.
Заметим, что
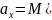 ),
a
),
a
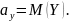 В
кач-ве статистики критерия возьмем
нормально распределенную СВ Z=
В
кач-ве статистики критерия возьмем
нормально распределенную СВ Z=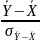 ,
где
,
где
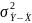 =
=
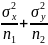 .
Если гипотеза
принимается, то критическая область
при ур-не знач-ти α определяется из
условия P(|z|>
.
Если гипотеза
принимается, то критическая область
при ур-не знач-ти α определяется из
условия P(|z|>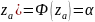 .
Если гипотеза
отвергается, те принимается гипотеза
при
.
Если гипотеза
отвергается, те принимается гипотеза
при
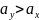 или
или
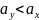 ,
то критическая область гипотезы
определяется из условий: P(z>
,
то критическая область гипотезы
определяется из условий: P(z>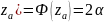 ;
P(z<-
;
P(z<-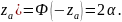 Рассмотрим случай, когда для нормально
распределенных СВ X
и Y
дисперсии
и
неизвестны. Предположим, что
Рассмотрим случай, когда для нормально
распределенных СВ X
и Y
дисперсии
и
неизвестны. Предположим, что
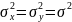 .
В кач-ве статистики для проверки гипотезы
:
.
В кач-ве статистики для проверки гипотезы
:
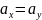 возьмем СВ T=
возьмем СВ T=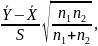 где
где
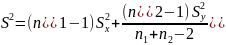 .
Критическая
область для принятия гипотезы
выбирается таким образом, чтобы P(T>
.
Критическая
область для принятия гипотезы
выбирается таким образом, чтобы P(T>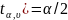 ,
P(T<-
.
Если гипотеза
отвергается, то используют рав-ва:
P(T>
,
P(T<-
.
Если гипотеза
отвергается, то используют рав-ва:
P(T>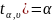 ,
P(T<-
.
,
P(T<-
.
