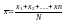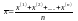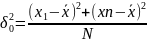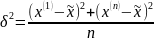19. Закон распределения Пуассона

Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то вместо формулы Бернулли пользуются приближенной формулой Пуассона 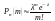, где 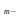число появлений события в n независимых испытаниях; m принимает значения 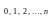. 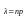(среднее число появлений события в n испытаниях). Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру 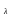, который определяет этот закон, т.е. .

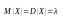20. Равномерный закон распределения

Непр. СВ Х называется распределённой по равномерному закону, если она принимает значения из (a,b] и если плотность её распределения имеет вид:

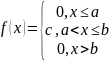
Так как с=1/b-a, то

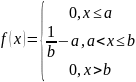
Функция распределения СВ Х:

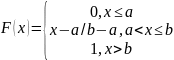
Числовые хар-ки:

М(Х)=(b+a)/2

D(X)=(b+a)² /12

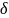(X)=b+a/2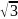

21. Закон нормального распределения

СВ Х наз. распределенной по нормальному закону, если ее плотность распределения имеет вид: 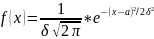, где >0, а – параметр распределения. Интеграл этой плотности распределения равен 1. Числовые характеристики: M(x)=a, 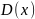= 2, = .

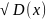22. Функция Лапласа и ее свойства

Функцией Лапласа называется функция вида: 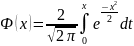. Свойства: 1) ф-я возрастает монотонно на (- ; 2) ф-я Лапласа нечетная: Ф(-х)=-Ф(х); 3) lim _x =1. Ф-я распределения:

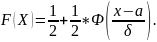
23. Вероятность попадания в интервал норм. распред СВ

Пусть СВ Х распределена по норм закону и ее функция распределения имеет вид . Вычислим p(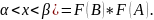 Получаем p( 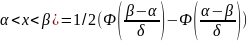- вероятность попадания в интервал. Найдем вер-ть того, что отклонение норм СВ от ее мат ожидания по модулю меньше некоторого положит числа 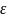р(|x-a|< ) и получаем

р(|x-a|< )= ).

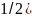24. Интегральная теорема Лапласа и ее следствие

Теорема: Пусть при каждом из n независимых испытаний, вероятность появления события А постоянно и равна р и отлична от 0 и 1 (n достаточно велико). Тогда вер-ть того, что число появлений соб А заключено между а и b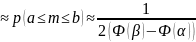 , где

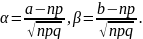
25. Неравенство Маркова

Пусть СВ Х принимает неотрицательное значение и у нее существует M(x), тогда каким бы ни было 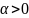всегда выполняется неравенство р(x . Это неравенство справедливо для любых СВ удовлетворяющих указанным двум требованиям.

26. Неравенство Чебышева

Теорема: пусть СВ Х имеет мат ожидание М(Х) и D(X), тогда какого бы ни было число , выполняется неравенство

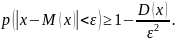
27. Теорема Чебышева

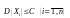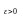
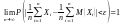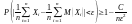Теорема: пусть х1,х2,хn независ СВ имеющие мат ожидание и дисперсиями, ограниченными одной и той же постоянной , то какова бы ни была постоянная . При доказательстве предельного равенства используется неравенств , которое вытекает из неравенства Чебышева.

28. Понятие о выборочном методе. Хар-ки ген и выбор совокупности

Статист. сов-тью называется сов-ть объектов, объединенных по какому-то признаку. Различают генер. и выборочную сов-ть. Выборочной сов-тью называется любая сов-ть случайно отобранных объектов. Ген. сов-тью наз сов-ть, из которой произведена выборка. Объемом сов-ти наз число объектов этой сов-ти. Выборка наз. повторной если объект перед отбором след. объекта возвращается в ген. сов-ть. Если не возвращается – бесповторной.

Пусть х1,х2,хn – знач-я в ген сов-ти (повтор-ся)	Пусть х(1),х(2),х(n) - значения признака А в выбор. сов-ти
Опр. число объектов ген. сов-ти наз объемом ген. сов-ти (N)	Опр. число объектов выбор сов-ти наз объемом выборки (n)
Ср. арифм.	Выбор. средняя
Ген дисперсия (cр. арифм. квадр отклонений значений признака сов-ти от ген средней)	Выбор. дисп-я
Ср. квадр. отклонение (арифм. корень ген дисперсии)	Выбор. ср квадр. отклонение δ
Ген. доля признака – отношение числа объектов облад. признаком А в ген сов-ти к объему ген совокупности p=M/N	Выбор. доля – отношение числа объектов облад. данным признаком в выборке к объему выборки w=m/n