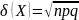12. Математическое ожидание и дисперсия дсв. Св-ва.
Математическим
ожиданием
ДСВ наз сумма произведений значений
СВ на соответствующие им вероятности.
М(X)=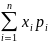
.
Св-ва:
1) Мат ожидание постоянной = самой
постоянной М(с)=с; 2) Мат ожидание суммы
2ух СВ = сумме мат ожиданий М(X+Y)=M(X)+M(Y);
3) Мат ожидание произведения 2ух
независимых СВ = произведению их мат
ожиданий M(X*Y)=M(X)*M(Y);
4) Постоянный множитель можно выносить
за знак мат ожидания M(k*X)=k*M(X);
5) M(X-Y)=M(X)-M(Y);
6) Мат ожидание отклонения СВ от ее мат
ожидания = 0 M(X-M(X))=0.
Дисперсия
– мера рассеивания значений СВ вокруг
своего среднего значения. Дисперсией
ДСВ наз мат ожидание квадрата отклонения
СВ от ее мат ожидания. D(X)=M(x-M(X))².
Арифметическое значение квадрата
отклонения из дисперсии наз средним
квадратическим отклонением
и обозначается σ(X)=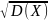
.
Cв-ва
дисперсии:
1) Дисперсия постоянной=0 D(c)=0;
2) Постоянный множитель можно выносить
за знак дисперсии возведя его в квадрат
D(k*X)
= k²*
D(X);
3) Дисперсия суммы 2ух независимых СВ =
сумме дисперсий D(X+Y)=D(X)+D(Y);
4) Дисперсия разности СВ = сумме дисперсий
D(X-Y)=D(X)+D(Y);
5) Формула вычисления дисперсий
D(X)=M(X²)-M²(X).
13. Числовые характеристики непрерывных св.
Пусть
непрерывная СВ задана плотностью
распределения f(x),
причем СВ принимает значения из
промежутка [a,b].
Отрезок a,
b
разобьем на n
произвольных частей, точками a=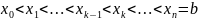
.
Длины частных отрезков обозначаются
через ∆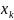
,
∆
,
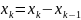k=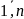
.
Длину наиболее из частных отрезков
обозначим через λ. На каждом частном
отрезке берем произвольную точку
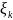и
вычислим вероятность p(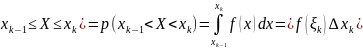
.
Составим
сумму
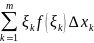(по
аналогии с суммой для ДСВ
).
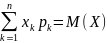Сумма является интегральной суммой
для ф-ии x*f(x)
на [a,b].
Если существует предел интегральной
суммы, при λ→0, то он наз мат
ожиданием
непрерывной СВ X
и обозначается M(X).
M(X)=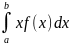
.
Дисперсия
непрерывной
СВ определяется также, как и дисперсия
ДСВ D(X)=M(x-M(X))²
=> D(X)=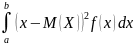
.
Среднее квадратическое отклонение
находится по формуле: σ(X)=
.
14. Формула Бернулли.
Несколько
повторных испытаний наз независимыми,
если вероятность того или иного испытания
не зависит от результатов других
испытаний. Пусть произведено n
независимых испытаний, вероятность
появления соб А постоянная и равна p,
те p(A)=p,
тогда вероятность соб p(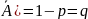
.
Определим вероятность
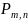того, что при n
испытаний соб А наступило ровно m
раз. Событие можно представить в виде
суммы произведений вида:
.
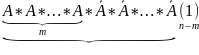Вероятность такого события определили
по теореме умножения вероятностей
независимых событий p(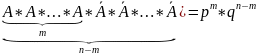
.
Произведений вида (1) будет столько
сколько существует способов выбора из
n
испытаний по m,
в кот соб А появилось, те
.
=>
–
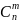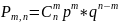ф-ла Бернулли.
15. Наивероятнейшая частота.
Частота,
кот соответствует наибольшая вероятность
в данной серии испытаний, наз
наивероятнейшей(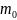
).
np-q≤
≤np+q.
Примечание: 1) правая часть отличается
от левой на 1 (np+p-np+q=p+q=1);
2) Если np-q
дробное число, то np+p
также дробное число. И
принимает одно значение; 3) Если левые
и правые части целые, то
принимает 2 значения
и
.
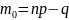16. Формула Пуассона.
Пусть
произведено n
испытаний, вероятность появления соб
А в каждом из этих испытаний равна p.
При достаточно больших n
и малых p
(0≤p≤0,1)
и при условии, что n*p=λ(λ-const),
имеет место приближенное рав-во:
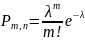– ф-ла
Пуассона или з-н редких событий.
17. Локальная теорема Лапласа.
Теорема:
Пусть при каждом из n
независимых испытаний вероятность
появления соб А постоянна, равна p
и отлична от 0 и 1. Тогда при достаточно
большом числе испытаний вероятность
того, что при этих n
испытаний соб А наступило ровно m
раз приближенно.
,
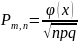где φ(x)=
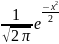– (ф-я
Гаусса) и x=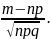
18. Биномиальный закон распределения
СВ
называется распределенной
по биномиальному закону,
если вероятность появления события А
в каждом испытании постоянна и равна
р, то число появлений события А —
дискретная случайная величина Х,
принимающая значения 0, 1, 2, …,
с вероятностями
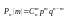(формула Бернулли), где
,
,
.
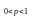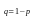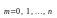Математическое ожидание и дисперсия
случайной величины Х, распределенной
по биномиальному закону, вычисляется
по формулам:
,
,
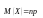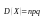