1. Элементы комбинаторики (размещения, перестановки, сочетания)

Размещениями из n элементов по m (m≤n) наз. подмножеством, сост. из m элементов и отлич. друг от друга эл-ми или порядком их расположения. 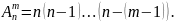Перестановка – размещения из n элементов по n. 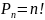Сочетаниями из n элементов по m (m<n) наз. такие размещения из n элементов по m, кот. различаются только элементам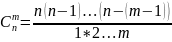и. или

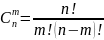
2. Событие. Виды случайных событий.

Событие – это результат опыта, испытания или наблюдения. Событие, кот. при испытании обязательно наступит, наз. достоверным (Ω). Событие, кот при испытании наступить не может, наз. невозможным (ø). Событие, кот. может наступить или не наступить, наз. случайным (A, B, C …). События А и В наз. несовместными, если появление одного из них исключает появление другого при одном и том же испытании. В противном случае они наз совместными. События наз единовременно возможными, если при испытании наступит хотя бы одно из этих событий. События наз равновозможными, если они имеют одинаковую возможность появиться. Два единственно возможных и несовместных события наз противоположными. Событие, противоположное событию А обознач. Ā.

3. Классическое и статистическое определение вероятностей. Св-ва.

Вероятностью события А наз отношение числа случаев благоприятствующих событию А к общему числу всех случаев. Обозн. 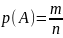, где m-число благоприятствующих случаев,n-общее число случаев. Св-ва: 1) Вероятность достоверного числа = 1(p(Ω)=1); 2) Вероятность невозможного числа = 0 (p(ø)=0); 3)Если событие А случайное, то 0<p(A)<1. Следствие: Вероятность любого события удовлетворяет неравенству: 0≤p(A)≤1.

Статист. опр-е вероятности: Пусть произведено n испытаний, при чем событие А появилось m раз. Число появлений события А при m испытаниях наз частотой события А. Отношение частоты к общему числу произведенных испытаний наз относительной частотой или частостью соб А (w(A)=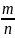 ). При маленьком числе испытаний частость носит случ хар-р и ее знач-я изм-ся от одной части к другой. При достаточно большом числе испытаний частотсти начинают группироваться вокруг числа, при чем чем ближе к этоиу числу, тем больше произведено испытаний. Число, вокруг кот группируются частости при достаточно большом кол-ве испытаний, наз статистической вероятностью соб А. На практике полагают, что стат вероятность соб А ≈ частости.

4. Теорема сложения вероятностей несовместных событий.

Суммой 2ух соб А и В наз соб А+В, состоящее в появлении хотя бы одного из этих событий. Если А и В несовместные события, то вместе они появиться не могут. Суммы 2ух несовместных соб А и В наз событием, сост в появлении одного из 2ух соб А или В. Теорема: Вероятность появления одного из 2ух несовм соб равна сумме вероятностей этих событий p(A+B)=p(A)+p(B). События 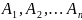образуют полную систему событий, если они единственно возможны и попарно несовместны ( те если наступает одно из этих событий). Теорема: Сумма вероятностей соб, образ-их полную систему соб равна 1(