50. Множественное уравнение регрессии.

Важн частный случай стат. связи – корреляцсвязь. При корреляц. связи разным значениям одной переменной соответ различные ср. значения др. перем-й, т.е. с изм-м знач признака х изменяется ср. значение признака у.

Множест корреляция – завис. результат. признака от двух и более факт-х признаков. Мат корреляц. зависимость результат. перем-й от неск. факторов опис ур-нием множеств. регр: y(x₁,x₂…x_k)= a+b_1.2…kx₁ +b_2.13…kx₂ +…+ b_k.12…k-1x_k

Уравнение множеств. регрессии характ ср. изменение y с измен признаков факторов. При построении уравнения множ регрессии нужно решить задачи: 1.Выбрать признаки – факторы, включенные в регрессию. 2.Выбрать тип уравнения регрессии.

Решение 1-ой задачи основыв-ся на рассмотрении матрицы парных коэфф корреляции и выделении тех переменных, для кот выполняется правило: Ryx_j > Rx_iy_j (где i≠j).

Реш 2-ой задачи основыв-ся на соотнош: чем проще тип ур-ния множеств. регрессии, тем очевиднее интерпретация его параметров, тем лучше для использ-ния регрессии с целью анализа и прогноза.

Параметры множеств. ур-ния регрессии так же, как и в парном уравнении регрессии расчитыв-ся МНК

å(y_i-a-b₁x₁-b₂x₂-…-b_kx_k)→min Получаем систему уравнений:

an + b₁åx₁+ b₂åx₂+_…+ b_kåx_k =åy

aåx₁ + b₁åx_i²+ b₂åx₁x₂+…+ b_kåx₁x_k =å yx₁

aåx_k + b₁åx₁x_k + b₂åx₂x_k+…+ b_kåx_k² =å yx_k

Отсюда a= y(ср.) - å b_j x_j(ср.) Коэфф b_j наз-ся коэфф-ми условно чистой регрессии. Термин условно-чистая регрессия означает, что каждая из величин b_j измер ср по совокупности отклон результ. признака от его ср. величины на ед-цу его измерения и при условии, что все прочие факторы, входящие в уравнение регрессии не изменяются и не варьируют.

Коэффициенты условно-чистой регрессии преобразуют в сравнимые величины. Полученные показатели наз-т стандартизир коэфф регрессии (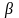 - коэфф). β_j= b_j*σ_xj / σ_{y, где} - коэфф показ на ск-ко отклоняется от своего ср. значения в ср квадр отклонениях результат. признак y при отклон факт. признака от своего ср. значения на 1 ср квадрат отклонение.

Коэфф эластичности показ на сколько % изменится результ. признак при измен факторного на 1%:Э_j= b_j*( x_j(ср.) / y_(ср.)).

Коэфф совокупной детерминации: R²=å Ryx_i β_iВ Вклад объясняющей переменной, кот измер коэфф раздельной детерм: D_i²= Ryx_i β_i

51. Оценка результатов корреляционно-регрессионного анализа

Частный случай стат. связи – корреляц связь.

Зад-й корреляц. анализа явл. колич. оценка тесноты связи м-ду призн.

З-ча регресс. анализа – опр-ние аналитич. выражения связи. Коррел- регресс. анализ включ измер тесноты связи и уст. аналитич. Выраж. связи.

Показатели корреляц. связи явл оценками той или иной законом-ти, поскольку в любом параметре сохр эл-т случайности. Поэтому необх стат. оценка ст-ни точности и надежности пар-ров корреляции и регрессии.

Надежность- вероят-ть того, что значение проверяемого парам-ра ≠0 и не включ-т в себя величины противопол-х знаков. Путем сравнения оценив величины со ср. случайной ошибкой оценки. Для коэфф парной регрессии(b) ср. ошибка оценки вычисл по ф-ле: где y^¯- знач-ния результ. признака, полученные по ур-нию регрессии; ∑(y_i-y¯)²/(n-2)- остат. дисперсия; (n-2)- число степеней свободы.

Зная ср. ошибку оценки коэф. регресии м. вычислить вер-ть того, что нулевое значение коэфф входит в интервал возмож с учетом ошибки значений. С этой целью нах-ся отн-ние коэф. к его ср. ошибке, назыв t-критерий Стьюдента: t=b/m_b. Если t расчетное > t таблич, то вероят-ть нулевого значения коэф. регрессии < ур-ня значимости (a) т.е. гипотезу о несущ этого коэфф можно отклонить. Надежность установленной связи: . 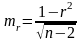Ср.ошибка условно чистого коэфф-та регрессии (b_j) рассчит по ф-ле: . Sост.-остаточное ср. кв. отклонение результ. признака. ; 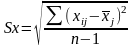. k- число ф-ров; n- ч-ло ед-ц совок-ти; i-№ ед-цы; j- номер ф-ра. Ср. ошибка оценки коэф множеств. 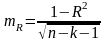корреляции: Оценка рез-тов регресс. анализа начин-ся с оценки суммар значимости рез-тов регресс. связи с пом. F-теста.

Цель теста: выяснить объясняют ли х-переменные значимую часть вариации у. Если этот тест значим- связь сущ и можно приступать к ее ислед. Нулевая гипотеза для F-теста утв-ет, что в генер. совок-ти м-ду х и у прогнозирующ взаимосвязь отсут. Если р-значение > 0.05, то полученный рез-т- незнач, <–значимый, если <0.01-высокознач.