47. Измер-е тесноты связи по результатам аналитической груп-ки

Аналитическая – групп-ка, выявл взаимосвязи м/д изуч явлениями и их признаками, из кот один признак явл результатом, другой (или другие) – фактором (напр., зависимость прибыли от оборачиваемости оборотных средств).

Для измерения тесноты связи м/д двумя признаками в случае линейной связи служит линейный коэф корреляции:

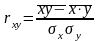
Линейный коэфф-т корреляции может принимать любые значения в пределах (-1;1). Чем ближе коээф корреляции по абсолютной величине к 1, тем теснее связь м/д признаками. Знак при лин-ом коээф-те корр-ции указывает на направление связи.

Сама по себе величина коэфф-та корр-ции не явл доказ-ом наличия причинно-следственной связи м/д признаками, а явл оценкой степени взаимной согласованности в изменениях признаков.

Установл причинно-след-ой связи должен предшест анализ качествен природы явления. Оценка степени тесноты связи с п-ю коэфф корреляции производ на основе более или менее огранич инф об изуч явл.

48. Показатель тесноты парной корреляционной связи.

Важнейший частный случай стат связи – корреляц связь. При корреляц. связи разным значениям одной переменной соответ различные ср. значения др. переменной, т.е. с изменением значения признака х изменяется ср значение признака у.

В ст-ке различ. виды зависимости:

1. парная корреляция – связь между 2мя признаками результат и факторным, либо м-ду двумя факторными.

2. частная корреляция – зависимость м-ду результативным и одним факторным признаком при фиксир. значении др. факторного признака.

3. множественная корреляция – зависимость результат. признака от двух и более фактор признаков.

Показателем тесноты связи в случае парной линейной корреляции явл линейный коэффициент корреляции r_xy . При расчете этого показателя учит значение отклонений индивид. значений признака от ср. величины соотв. для факторного признака х(i)–х(cр.), для результ признака y(i)–y(ср.)

Непосредственно сопоставить м-ду собой полученные величины нельзя, т.к. сами признаки м.б. выражены в разных единицах, но при наличии одних и тех же единиц измерения ср могут различ по величине. В этой связи сравнению могут подлежать отклонения, выраж в относительных величинах, т.е. в долях ср квадратич отклонения.

Их наз нормированными отклонениями. Для факторного признака t(x)=x(i)-x(ср.)/ δ(x), для результативного признака. t(y)=y(i)-y(ср.)/ δ(y)

Ср величина из произведения нормир отклонений и будет яв-ся линейным коэфф кор-реляции. R(xy)=∑t(x)t(y)/n=∑(x(i)-x(ср.))*(y(i)-(cр.))/nδ(x),

δ(y), R(xy)= xy(ср)-x(ср)y(ср) / δ(x)δ(y)

Линейный коэф. корреляции может принимать любые знач в пределах от –1 до +1. Чем ближу к 1 – тем теснее связь между признаками. Знак при коэф. укаывает на направление связи.

Квадрат коэфф корреляцц R²(ху) наз. коэф-том детерминации и показ. долю вариации результат. признака объясняемую вариацией фактор. признака. Он принимает значения в интервале (0,1). Чем ближе к 1, тем теснее связь.

49. Определение параметров уравнения парной регрессии.

Важн частный случай стат. связи – корреляционная связь. При корреляц. связи разным значениям одной переменной соответствуют различные ср. значения др. переменной, т.е. с изменением значения признака х изменяется ср. значение признака у.

В статистике принято различать виды зависимости:

1. парная корреляция – связь между 2^мя признаками результативным и факторным, либо м-ду двумя факторными.

2. частная корреляция – зависимость м-ду результативным и одним факторным признаком при фиксир. значении др. факторного признака.

3. множественная корреляция – зависимость результат. признака от двух и более факторных признаков.

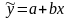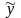Уравнение парной линейной корреляц связи наз уравнением парной регрессии и имеет вид . Где - ср. значение разультат признака y, при определеных значениях признака x; a – свободный член уравнения; b – коэф регрессии, показывает вариацию приз-нака y, приходящуюся на единицу вариации x.

Параметры уравнения находятся с помощью МНК. Исходным МНК для прямой линии является следующее:

С помощью преобразований получаем систему нормальных уравнений.