Флуктуирующая пачка.

Будем полагать, что амплитуда импульсов в пачке флуктуирует независимо друг от друга, согласно закону Релея. Начальная фаза случайна и независима и изменяется равномерно от 0 до 2п.

Так же как и в предыдущее случае отношение правдоподобия рассматривается как n отношений правдоподобия одиночных импульсов.

полагая, что все импульсы имеют одинаковую энергию, получим:

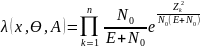
После логарифмирования получаем:

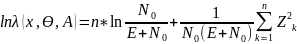
Единственная операция, связанная с действием над принятым сигналом – это на хождение этой суммы. Поэтому структура устройства обработки флуктуирующей пачки импульсов отличается квадратичной характеристикой детектора.

Таким образом, оптимальная обработка сигналов в виде пачки нефлуктуирующих и независимо флуктуирующих импульсов со случайными начальными фазами сводится к пропусканию принятого сигнала через фильтр, согласованным с одиночным радиоимпульсом и суммированию всех продетектированных реализаций. Процедура оптимального обнаружения завершается сравнением накопленного на сумматоре напряжения с пороговым значением.

Устройство оптимальной обработки пачек некогерентных радиоимпульсов.

Методика вычисления D и F по оптимальной обработке пачек некогерентных радиоимпульсов сводится к :

1. производится вычисление закона распределения вероятности амплитуды одиночного импульса на выходе детектора о присутствии шума. Если сигнал является нефлуктуирующей пачкой, то в качестве оптимального может быть принят линейный детектор. Тогда распределение напряжения на выходе совпадает с распределением огибающей. Тогда напряжение огибающей подчиняется закону распределения Релея. Если пачка флуктуирует, необходимо найти закон распределения квадрата огибающей.

2. находим плотность вероятности напряжения на выходе сумматора.

3. Зная закон распределения каждого из n слагаемых, находим плотность вероятности их суммы (при наличии одного шума и при условии наличия и полезного сигнала).

4. Интегрируем плотности вероятности в пределах от Z0 до бесконечности. Находим D и F.

Понятие среднего риска и статистические критерии обнаружения.

В общем требования к оптимальному приемнику обнаружения должны быть выработаны с учетом относительной опасности каждого из возможных ошибочных решений. В таких случаях используется понятие среднего риска, которое позволяет сформулировать единые статистические критерии обнаружения.

Введем понятие среднего риска на примере радиолокационного обнаружения цели.

При обнаружении цели возможны 4 ситуации:

1. правильное обнаружение с вероятностью P1=W(x1)*D

2. правильное обнаружение с вероятностью p2=W(x0)*Ḟ

3. пропуск цели с вероятностью P3=W(x1)Ď

4. ложная тревога с вероятностью P4=W(x0)F

Эти ситуации представляют собой полную группу случайных событий, поэтому сумма их вероятностей =1.

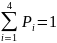
Каждой из ситуаций может быть приписана определенная плата за ошибку в зависимости от стоимости или опасности.

Правильным решением лучше приписывать нулевую плату, а ошибочным тем большую, чем опаснее последствие. Так как каждая ситуация имеет случайный характер, вводится средняя плата в виде математического ожидания.

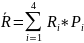
P_i – плата за i-ю ситуацию

R_f – плата за ложную тревогу

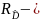плата за ошибку пропуска цели

Подставляем плату в формулу и получаем:

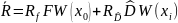
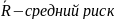
Система обработки принятого колебания y(t) минимизирует средний риск устройством оптимальной обработки сигнала.

Критерий минимума среднего риска – наиболее общий из всех статистических критериев обнаружения. Большинство известных статистических критериев представляют собой частные случаи критерия минимума среднего риска.

Если выполняется условие 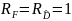, то средний риск дает значение суммарной вероятности ошибок обнаружения. Условие минимума суммарной вероятности ошибок обнаружения носит название «критерий идеального наблюдателя» (КИН). КИН не учитывает относительной стоимости ошибок ложной тревоги и пропуска цели и является менее общим.

Если выполняется условие W(x1)=W(x0) КИН сводится к условию минимизации условной вероятности ошибочного решения.

Этот критерий носит название критерия максимального правдоподобия.

Из этого выражения следует правило принятия решения, удовлетворяющее критерию максимума правдоподобия.

Критерий максимального правдоподобия (КМП) не требует знания априорной вероятности наличия или отсутствия цели.

Минусы этого критерия как и КИН является разная стоимость ошибок ложной тревоги и пропуска цели.

Часто вероятность ложной тревоги не должна превышать заданной. Априорные вероятности наличия и отсутствия цели неизвестны.

В таких случаях желательно иметь приемник, обеспечивающий максимальную вероятность правильного обнаружения цели при заданном F. Это критерий Неймана- Пирсона.

Выбор критериев определяется задачами, которые решает РЛС.

Критерий Неймана-Пирсона используется при радиолокационном обнаружении.

КИН соответствует задачам с системах связи. КНП применяется если априорные вероятности не заданы, а ложная тревога и пропуск одинаково опасны.

Реализация любого критерия основана на вычислении отношения правдоподобия, а различная трактовка условий оптимальности выливается в выбор значения .

1. В подходе предполагалось, что в распоряжении наблюдателя 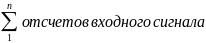, которые определяют y(t)на интервале Т. Для вычисления отношения правдоподобия используются все n независимых отсчетов. Следовательно время наблюдения будет фиксирована и равно Т.

2. Возможен иной подход к решению. Последовательно на каждом этапе вычисляется отношение правдоподобия. Для каждого отсчета вычисляется 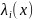– это отношение правдоподобия сравнивается с двумя пороговыми значениями.

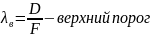
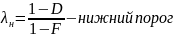
Решение о наличии цели принимается сразу при превышении верхнего порога. Решение об отсутствии цели принимается при пересечении нижнего порога.

Если отношение правдоподобия в зоне неопределенности между 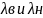, вычисление продолжается- это последовательный анализ. Время наблюдения является случайной величиной. Среднее время наблюдения зависит от , определяется вероятностями D и F.

Последовательный анализ – оптимальная процедура обнаружения, так как минимизирует среднее время наблюдения при постоянных D и F – это критерий последовательного наблюдателя. Он применяется в импульсных РЛС, радионавигационных системах. В этом случае сигнал – это последовательность импульсов.

1