31)Температурная зависимость удельного сопротивления металлов:

У металлов, не обладающих сверхпроводимостью, при низких температурах из-за наличия примесей наблюдается область 1 – область остаточного сопротивления, почти не зависящая от температуры (рис. 10.5). Остаточное сопротивление  _ост тем меньше, чем чище металл.

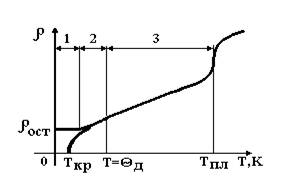
Рис. 10.5. Зависимость удельного сопротивления металла от температуры

Быстрый рост удельного сопротивления при низких температурах до температуры Дебая _д может быть объяснен возбуждением новых частот тепловых колебаний решетки, при которых происходит рассеяние носителей заряда - область 2.

При Т > _д, когда спектр колебаний возбужден полностью, увеличение амплитуды колебаний с ростом температуры приводит к линейному росту сопротивления примерно до Т_пл - область 3. При нарушении периодичности структуры электрон испытывает рассеяние, приводящее  к изменению  направления движения, конечным длинам свободного пробега и проводимости  металла. Энергия  электронов  проводимости  в металлах составляет 3–15 эВ, что соответствует длинам волн 3–7 Å. Поэтому любые нарушения периодичности, обусловленные примесями, дефектами, поверхностью кристалла или тепловыми колебаниями атомов (фононами) вызывают рост удельного сопротивления металла.

Проведем качественный анализ температурной зависимости удельного сопротивления металлов.  Электронный газ в металлах является вырожденным и основным механизмом рассеяния электронов в области высоких температур является рассеяние на фононах.

При понижения температуры до абсолютного нуля сопротивление нормальных металлов стремится к постоянному значению  остаточному сопротивлению. Исключением из этого правила  являются сверхпроводящие  металлы и сплавы, в которых сопротивление исчезает ниже некоторой критической температуры Т_св (температура перехода в сверхпроводящее состояние).

При увеличении температуры, отклонение удельного сопротивления от линейной зависимости у большинства металлов наступает вблизи температуры плавления Т_пл. Некоторое отступление от линейной зависимости может наблюдаться у ферромагнитных металлов, в  которых происходит дополнительное рассеяние электронов на нарушениях спинового порядка.

При достижении температуры плавления и переходе в жидкое состояние у большинства металлов наблюдается резкое увеличение удельного сопротивления и у некоторых его уменьшение. Если плавление металла или сплава сопровождается увеличением объема, то удельное сопротивление повышается в  два–четыре  раза (например, у ртути в 4 раза).

У металлов, объем которых при плавлении уменьшается,  наоборот, происходит понижение удельного сопротивления (у галлия на 53%, у сурьмы –29% и у висмута –54%) . Подобная аномалия может быть объяснена возрастанием плотности и модуля сжимаемости при переходе этих металлов из твердого в жидкое состояние. У некоторых расплавленных (жидких) металлов удельное  сопротивление с ростом температуры при постоянном объеме перестает расти,  у других оно растет более медленно, чем в твердом состоянии. Такие аномалии, по-видимому, можно связать с явлениями разупорядочения решетки, которые неодинаково происходят в различных металлах при переходе их из одного агрегатного состояния в другое.

Важной характеристикой металлов  является температурный коэффициент удельного электрического сопротивления, показывающий относительное изменение удельного сопротивления при изменении температуры на один Кельвин (градус)

(10.11)

_положительно, когда удельное сопротивление возрастает при повышении температуры. Очевидно, что величина  _  также является функцией температуры.  В области 3 линейной зависимости  (T) (см. рисунок 10.3) выполняется   соотношение:

1

(10.12)

где  _ и _ удельное сопротивление и температурный коэффициент удельного сопротивления при температуре  _, а    удельное сопротивление при температуре T. Экспериментальные данные показывают, что у большинства металлов _ при комнатной температуре примерно 0,004 К^-1.У ферромагнитных металлов значение _ несколько выше.

32)Влияние примесей и дефектов структуры на проводимость металлов.Правила Матисена, Линде

Как отмечалось, причинами рассеяния электронных волн в металле

являются не только тепловые колебания узлов решетки, но и статические

дефекты структуры, которые также нарушают периодичность потенциального

поля кристалла. Рассеяние на статических дефектах структуры не зависит от

температуры. Поэтому по мере приближения температуры к абсолютному нулю

сопротивление реальных металлов стремится к некоторому постоянному значению,

называемому остаточным сопротивлением. Отсюда вытекает правило Маттиссена

об аддитивности удельного сопротивления:

(16)

т. е. полное сопротивление металла есть сумма сопротивления, обусловленного

рассеянием электронов на тепловых колебаниях узлов кристаллической решетки,

и остаточного сопротивления, обусловленного рассеянием электронов на

статических дефектах структуры. Иcключение из этого правила составляют

сверхпроводящие металлы, в которых сопротивление исчезает ниже некоторой

критической температуры.

Наиболее существенный вклад в остаточное сопротивление вносит рассеяние

на примесях, которые всегда присутствуют в реальном проводнике либо в виде

загрязнения, либо в виде легирующего (т. е. преднамеренно вводимого) элемента.

Следует заметить, что любая примесная добавка приводит к повышению ρ, даже

если она обладает повышенной проводимостью по сравнению с основным металлом. Так, введение в медный проводник 0.01 ат. доли примеси серебра

вызывает увеличение удельного сопротивления меди на 0.002 мкОм·м.

Экспериментально установлено, что при малом содержании примесей удельное

сопротивление возрастает пропорционально концентрации примесных

атомов.

температурные зависимости удельного сопротивления чистой меди и ее сплавов с малым количеством (приблизительно до 4 ат. %) индия, сурьмы, олова,

мышьяка взаимно параллельны; для сплавов с переходными металлами

наблюдаются и некоторые отклонения от этого правила.

Одна из причин отклонений от правила Маттиссена может быть связана с

влиянием примесей на упругие свойства металла, что сопровождается изменением

колебательного спектра кристаллической решетки.

Помимо примесей некоторый вклад в остаточное сопротивление, вносят

собственные дефекты структуры – вакансии, атомы внедрения, дислокации,

границы зерен. Концентрация точечных дефектов экспоненциально

возрастает с температурой и может достигать высоких значений вблизи

точки плавления. Кроме того, вакансии и междоузельные атомы легко возникают в материале при его облучении частицами высокой энергии,

например, нейтронами из реактора или ионами из ускорителя. По

измеренному значению сопротивления можно судить о степени

радиационного повреждения решетки. Таким же образом можно проследить

и за восстановлением (отжигом) облученного образца.

Изменение остаточного сопротивления меди на 1 ат. % точечных

дефектов составляет: в случае вакансий 0.010 – 0.015 мкОм·м; в случае атомов

внедрения 0.005 – 0.010 мкОм·м.

Если имеется несколько механизмов рассеяния, каждый из которых не влияет на другие, то полная вероятность рассеяния

W =  iWi.

(10.1)

  В приближении времени релаксации:

1/  =   i 1/ i.

(10.2)

Предположим, кроме того, что время релаксации для каждого механизма не зависит от k. Тогда

= m/(ne2 ) = m/(ne2)  i 1/ i =   i i .

(10.3)

Это т.н. правило Матиссена: удельное сопротивление = сумме парциальных удельных сопротивлений, обусловленных каждым механизмом. Ограниченность этого правила связана с предположениями а) о независимости механизмов, б)  (k) = const. Можно показать, что правило Матиссена выполняется как неравенство:

>  i  i.