5.4. Предел функции

По аналогии с определением предела последовательности при n   введем сначала определение предела функции при х .

Число b называется пределом функции f(x) при х , если для любого положительного числа e найдется такое число М = М(e), что для всех х М, выполняется неравенство:f (x)- b e .

Другими словами: число b называется пределом функции при х , если при всех х, удаляющихся в бесконечность значения функции неограниченно приближаются к b.

Записывают так: f(х) = b.

Число b называется пределом функции f(х) в точке а ( или при х стремящемся к а ), если для любого   0 существует  = (), зависящее от , такое, что для всех х  , удовлетворяющих неравенству х – а, справедливо неравенство  f(х) - b .

Другими словами: число b называется пределом функции при х а, если при всех х, неограниченно приближающихся к а, значения функции неограниченно приближаются к b.

Записывают так: f(х) = b.

Проще: передел функции y = f(x) при стремлении х к а есть число b, к которому приближается значение у с любой наперед заданной точностью.

Геометрическая иллюстрация.

y = f(х)  x-a ,



a-  x  a+,

 f(х) - b ,



b-  f(х)  b+.

Можно доказать:

1. Если функция имеет конечный предел, то этот предел единственный.

2. = С, С = const;

3. х = а.

Часто рассматриваются пределы функции, если х а и при этом х  а: f(x) – предел слева;

или х а и х  а: f(x) – предел справа.

Изучаются и другие пределы функций, например:

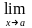f(х) = + ; f(х) = - ;

f(x) = + ; f(x) = - ;

f(х) = + и т. п.

Теорема 1. Предел алгебраической суммы конечного числа функций равен алгебраической сумме пределов этих функций

.

Доказательство: Для доказательства достаточно рассмотреть две функции, это не нарушит общности рассуждений. Пусть , .

По теореме о связи функции, её предела и бесконечно малой, функции и можно представить в виде где и – бесконечно малые при .

Найдём сумму функций и

Величина есть постоянная величина, 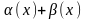– величина бесконечно малая. Таким образом, функция представлена в виде суммы постоянной величины и бесконечно малой функции.

Тогда число является пределом функции , т.е. .Теорема доказана.

Теорема 2. Предел произведения конечного числа функций равен произведению пределов этих функций .

Доказательство: Не нарушая общности рассуждений, проведём доказательство для двух функций и . Пусть , тогда , Найдём произведение функций и

Величина есть постоянная величина, бесконечно малая функция. Следовательно, число является пределом функции , то есть справедливо равенство . Следствие: .

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля .

Доказательство: Пусть 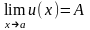, Тогда , .

Найдём частное и проделаем над ним некоторые тождественные преобразования

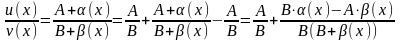
Величина постоянная, дробь бесконечно малая. Следовательно, функция представлена в виде суммы постоянного числа и бесконечно малой функции.

Тогда .

Замечание. Теоремы 1–3 доказаны для случая . Однако, они могут быть применимы при , поскольку доказательство теорем в этом случае проводится аналогично.

Теоремы о пределах.

Пусть существуют и конечны f(х) = А; g(x) = В, тогда

1) (f(x) g(x)) = f(x) g(x) = А В;

предел суммы (разности) функций равен сумме (разности) их пределов:

2. предел произведения функций равен произведению их пределов:

(f(x) g(x)) = ( f(x))( g(x)) = АВ;

следствие: постоянный множитель можно вынести за знак предела:

(С f(x)) = С f(x), С = const,

3) предел отношения двух функций равен отношению их пределов, если предел делителя отличен от нуля:

; В  0.

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

Пусть на некотором числовом множестве задана числовая функция и число — предельная точка области определения . Существуют различные определения для односторонних пределов функции в точке , но все они эквивалентны.