Бесконечно малые и бесконечно большие величины

О п р е д е л е н и е 1. Функция y = f (x) называется бесконечно малой величиной (Б.М.В.) при , если ее предел равен нулю

                                 (4.10)

Геометрически это означает, что функция y = f (x) либо пересекает ось ОХ (рис. 65а), либо касается ее в точке x = a (рис. 65б).

а)	б)
Рис. 65

О п р е д е л е н и е 2. Функция y = f (x)  называется бесконечно малой величиной при , если для каждого положительного сколь угодно малого числа найдется положительное число , такое, что для всех х, удовлетворяющих неравенству , будет выполняться неравенство .

О п р е д е л е н и е 3. Функция  y = f (x) называется бесконечно малой величиной при , если для каждого положительного сколь угодно малого числа найдется сколь угодно большое положительное число такое, что для всех х, удовлетворяющих неравенству будет выполняться неравенство (рис. 66). .      (4.11)

Рис. 66

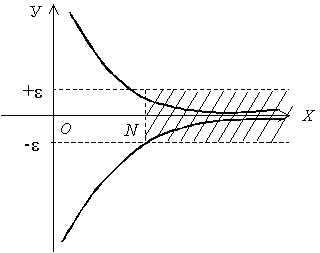
Геометрически: для всех значений х, которые , значения функции попадают в -окрестность нулевой точки:

Рис. 67

О п р е д е л е н и е 4. Функция y = f (x)   называется бесконечно большой величиной при , если для каждого положительного сколь угодно большого числа N найдется соответствующее сколь угодно малое положительное число y = f (x)  такое, что для всех х, удовлетворяющих неравенству , будет выполняться неравенство : .          (4.12) Геометрически: для всех значений х, попадающих в -окрестность точки а , соответствующие значения функции будут по абсолютной величине больше сколь угодно большого числа N (рис. 67):

                                      (4.13)

О п р е д е л е н и е 5. Функция y = f (x)  называется бесконечно большой величиной при , если для каждого положительного сколь угодно большого числа N найдется соответствующее сколь угодно большое число K(N) такое, что для всех х, удовлетворяющих неравенству , будет выполняться неравенство :

.                                                       (4.14)

Рис. 68

Геометрически: Функция y = f (x) будет бесконечно большой величиной при , если функция может принимать значения по абсолютной величине больше наперед заданного числа N (рис. 68):      (4.15)

В ы в о д ы:

1. Функция  y = f (x) является бесконечно большой величиной, если

   или    .                      (4.16)

2. Данная запись (4.15) является символической.

3. Понятия бесконечно большая величина и бесконечно малая величина относятся только к характеру поведения функции, а не к ее величине вообще.

4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними

Пусть f₁ (x)  и   f ₂ (x) бесконечно малые величины при , т.е.      и      .

1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:

.                      (4.17)

2. Произведение бесконечно малых величин есть величина бесконечно малая:

.                           (4.18)

3. Произведение бесконечно малой величины на константу С или на функцию, имеющую конечный предел , есть величина бесконечно малая:

.                       (4.19)

Пусть и бесконечно большие величины при , т.е.       и     .

1. Сумма бесконечно больших величин есть величина бесконечно большая:

.                                                   (4.20)

2. Произведение бесконечно больших величин есть величина бесконечно большая:

.                                                   (4.21)

3. Произведение бесконечно большой величины на константу С, или на функцию, имеющую конечный предел , есть величина бесконечно большая:

                      (4.22)