Четные и нечётные функции.

Область определения функции называется симметричной, если для любого х из области определения функции существует ( -х ) тоже принад-лежащий этой области.

Функция у = f(х) называется четной, если она имеет симметричную область определения и для всех х из этой области выполняется равенствоf(-х) = f(х)

Функция у = f(х) называется нечетной, если она имеет симметричную область определения и для всех х из этой области выполняется равенствоf(-х) = - f(х)

Графики четных функции симметричны относительно оси ординат, гра-фики нечетных функций симметричны относительно начала координат.

Например: функции у = х², y = x⁴ - четные ( рис 1.1 ), а функции у = х³, у = х - нечетные ( рис 1.2 ).

Периодические функции.

Функция у = f(х) называется периодической, если существует такое число Т ≠ 0, что вместе с любым х из области определения функции точки (х + кТ) тоже принадлежат этой области и при этом выполняется неравенство

f(х) = f(х + кТ ). Число Т называется периодом функции.

Например у = sin x периодическая функция с периодом Т = 2π. (рис 1.9 ).

Ограниченные функции.

Функция у = f(х) называется ограниченной сверху в некоторой области значений аргумента, если существует такое число М, что для всех х из этой области f(х) ≤ М.

Функция у = f(х) называется ограниченной снизу в некоторой области, если существует такое число N, что для всех х из этой области f(х) ≥ N.

Функция называется ограниченной, если она ограничена снизу и сверху.

Например: функция у = ограничена снизу числом 0 (рис. 1.3 )

функция у = 2 –х² ограничена сверху числом 2

функция у = sin x ограниченная │sin x│≤ 1 (рис. 1.9 ).

Монотонные функции. Экстремум функции.

Функция у = f(х) называется возрастающей на промежутке (а, b), если для любых х₁ и х₂ из этого промежутка из неравенства х₂ > х₁ следует неравенство f(х₂) > f(х₁), то есть большему значению аргумента соответствует большее значение функции.

Функция у = f(х) называется убывающей на промежутке (а, b), если для любых х₁ и х₂ из этого промежутка из неравенства х₂ > х₁ следует неравенство f(х₂) < f(х₁), то есть большему значению аргумента соответствует меньшее значение функции.

Возрастающие и убывающие функции называются монотонными.

Например: Функция у = х³ возрастает на всей области определения

Функция у = х² возрастает на интервале ( 0, +∞ ) и убывает на интервале

( - ∞, 0 ).

Точка х₀ называется точкой максимума функции у = f (х), если существует такая двусторонняя окрестность точки х₀, что для всех х из этой окрестности выполняется неравенство f (х₀) > f(х)

Точка х₀ называется точкой минимума функции у = f(х), если существует такая двусторонняя окрестность точки х₀, что для всех x из этой окрестности выполняется неравенство f(х₀) < f(х).

Значение функции в точке максимума называется максимумом функции, а значение функции в точке минимума называется минимумом функции. Обозначается соответственно y_max,, у_min.

Точки максимума и минимума называются точками экстремума.

Понятия функциональной зависимости широко используются в экономических моделях (задачах). Посредством элементарных функций и их графиков моделируются взаимосвязи между многими экономическими характеристиками и показателями. Спектр элементарных функций используемых в экономике довольно широкий:

• Линейные; Дробно-линейные; Степенные; Показательные; Логарифмические.

Наибольшее распространение имеют функции спроса (или потребления) отражающие зависимость спроса от комплекса факторов, влияющих на него. Примером такой зависимости служит дробно-линейная функция Торнквиста .

Эта функция описывает зависимость величины спроса на предметы первой необходимости от величины доходов 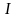. Соответствующие этим функциям кривые называются кривыми Энгеля по имени впервые изучившего их немецкого ученого.

Для построения графика этой функции достаточно преобразовать ее к виду:тт

График функции может быть построен растяжения в раз гиперболы и последующим сдвигом полученной кривой вдоль координатных осей.

Другим примером функции в экономике служат функции спроса и предложения для соотношения спроса и цен. Известно, что для большинства благ действует зависимость: чем выше цена, тем ниже спрос, и наоборот. Здесь возможны различные типы зависимости и, следовательно, различные формы кривых.

Производственная функция – это экономико-математическая функция, связывающая переменные величины затрачиваемого или используемого ресурса (фактора производства) с величинами (объемами) выпускаемой продукции.

Аналитическая запись в производственной функции означает, что если ресурс затрачивается или используется в объеме единиц, то продукция выпускается в объеме единиц. Закон в данном случае, являясь характеристикой производственной системы, отображает независимую переменную «ресурс» в зависимую переменную «выпуск». Однако следует заметить, что такая трактовка производственной функции имеет смысл только в микроэкономической теории, где под понимается максимально возможный объем выпуска продукции, при затрачиваемом ресурсе в единиц. В макроэкономической теории такая модель не совсем корректна.

В микро экономике производственная функция чаще всего записывается в виде степенной функции , где - величина затрачиваемого ресурса (например, затрачиваемого времени), - объем выпускаемой продукции ( например, количество обработанной информации). Числа и называются параметрами производственной функции. Графиком однофакторной производственной функции служит кривая

Интерпретация полученной кривой отражает фундаментальное положение экономической теории, которое называется законом убывающей эффективности. На графике хорошо видно, что с ростом величины затрачиваемого ресурса объем выпуска продукции растет, однако при этом каждая дополнительная единица ресурса дает все меньший прирост объема выпускаемой продукции.