Исследование кривых,заданных параметрами. Пусть , исследуем ан. Вычисляем и .Для точек кривой, вблизи которых кривая является графиком некоторой функции , вычисляем .
Находим
,
при которых хотя бы одна из
или
обращается в нуль или терпит разрыв,
следовательно,
- критические точки. Затем в любом
интервале
,
(а следовательно, и в любом
)
определяем знак
и тем самым находим области возрастания
и убывания
.
Это даёт также возможность определить
характер точек, соответствующих
.Далее находим
и
исследуя на знак, определяем направления
выпуклости кривой на любом интервале. Для
нахождения асимптот находим такие
,
что при
или
или
,
или и
и
.
Пример. 
(1’)
и
опр. для
,
но в силу периодичности
.
Тогда
и
кривая
асимптот не имеет.
Далее (*)
при
(**)
-
обл. изм. t
x
y
Знак
убыв., возр.
-
убыв.
+
возр.
-
убыв.
+
возр.
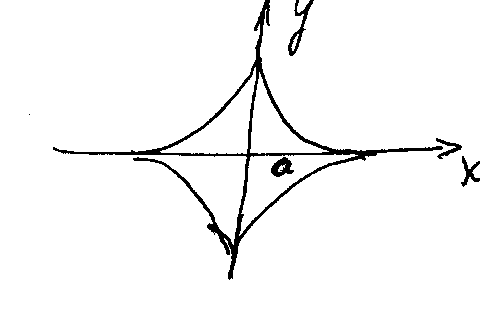Из
таблицы следует, что (1) определяет 2
непрерывных
:
при
и при
.
Из (**) следует, что
и
,
т.е. в этих точках касательная к
вертикальна.
В точках же
,
т.е. касательная к
- горизонтальна. Далее
:
при
- кривая вогнутая,
при
- кривая выпуклая. (астроида)
Общий план исследования функций и построения графиков.
Под «исследованием функции» обычно понимается нахождение:
естественной области существования функции;
точек разрыва функции; нули функции?
интервалов возрастания и убывания функции;
точек максимума и минимума и экстремальных значений функции;
областей выпуклости и вогнутости графика, точек перегиба;
асимптот графика функции.
На основании проведённого исследования строится график. Целесообразно помечать элементы графика параллельно с исследованием.
Замечание
1. Если
- чётная, т.е.
достаточно
исследовать
и строить её график для
ОДЗ,
т.к. график симметричен OY.
Замечание
2. Если
- нечётная, т.е.
также
достаточно провести исследование для
.
График симметричен относительно начала
координат.
Замечание 3. Т.к. одни свойства функции могут определять другие, то порядок исследования можно изменять, исходя из конкретного вида исследуемой функции. Например, если непрерывна и дифференцируема и найдены точки максимума и минимума, то тем самым определены области убывания и возрастания.
Элементы дифференциальной геометрии.Касательная и нормаль к плоской кривой.
Как
было показано раньше, уравнение
касательной к кривой
в точке
,
которая называется точкой касания,
имеет вид:
,где
Определение. Прямая, проходящая через точку касания перпендикулярно к касательной, называется нормалью к кривой .
Используя
условие перпендикулярности двух прямых,
нетрудно вывести уравнение нормали:
или
.
Пример
1. Найти уравнение касательной и нормали
к
в точке
.
Дифференцируя,
получим
и
.
Уравнение
касательной
или
,
т.к.
.
Уравнение
нормали
или
.
Пример 2. Касательная и нормаль к циклоиде:
Касательная
и нормаль в точке
будут иметь уравнения:
- касательная
- нормаль
К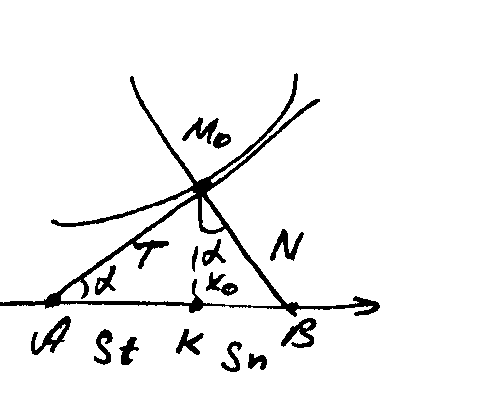
асательная
и нормаль кривой, проведённые в
,
в пересечении с OX
образуют
.
Катеты этого треугольника -
и
,
отрезки
и
,
на которые ордината
делит гипотенузу
,
часто используют в различных вопросах
геометрии и получили специальные
обозначения и названия:
- длина касательной, 
- длина нормали, 
- подкасательная, 
- поднормаль.
Все
эти отрезки лкгко могут быть вычислены
через
и
в точке
.
В
:
.
Поэтому:
или
Знаки модуля введены потому, что и могут быть меньше нуля.
Пример.
Доказать, что
- поднормаль
имеет для всех точек параболы одну и ту
же длину. 
имеет
подкасательную -
.
.