Разложение по формуле Тейлора функций

1. . В первую очередь найдём значения при

Подставляя эти значения в формулу (**) Маклорена, получим

, где .

Если , то взяв , получим оценку остаточного члена

При , получается формула, позволяющая найти приближённое значение числа :

Здесь ошибка не превосходит или .

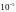Отметим, что для остаточный член при .

Действительно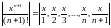

Т.к. - фиксированное число, . Введём обозначение При , и т.д., можно написать

Но есть const, не зависящая от n, а при

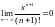Следовательно, и

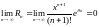
Т.о. для мы можем вычислить с любой степенью точности, взяв достаточно большое n.

2.

Подставляя теперь эти значения в формулу Тейлора, получим

.

Т. к .

Применим полученную формулу для , положив .

Оценим теперь остаточный член:

Следовательно, ошибка меньше чем или с точностью до .

3. .

,

(х – в радианах).

Исследование функции на максимум и минимум с помощью формулы Тейлора.

Ранее мы показали, что если при может быть либо max, либо min, либо нет ни того, ни другого. Покажем, как в это случае может быть использована формула Тейлора.

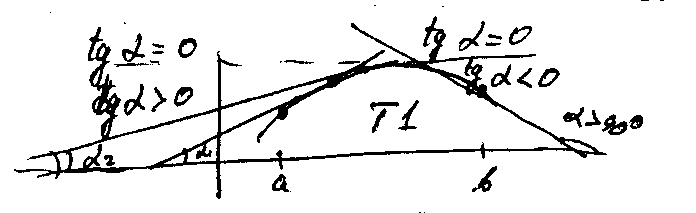
Предположим, что при x=a

(1)

Пусть также f(x) имеет непрерывные производные до (n+1)-го порядка включительно в окрестности x=a. Запишем для f(x) формулу Тейлора, учитывая (1):

(2)

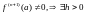Т.к. непрерывна в окрестности x=a и , что при . При этом, если 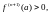то и во всех точках интервала будет и если и . Перепишем (2) в виде:

(2’)

и рассмотрим различные возможные случаи.

1. n – нечётное

а) . Тогда в интервале , и т.к. . Т.к. чётное число и правая часть (2’) <0. Следовательно, точка максимума .

б) , т.к. точка минимума .

2. n – чётное

Тогда n+1 – нечётное, и имеет разные знаки при и .

Если h достаточно мало по модулю, то -я производная сохраняет знак во всех точках . Следовательно, имеет разные знаки при и , а это означает, что в нет ни максимума, ни минимума .

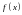Таким образом, если при имеем: 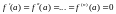, и первая не обращающаяся в 0 производная есть производная чётного порядка, то в

имеет максимум, если и

имеет минимум, если .

Если же 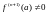есть производная нечётного порядка, то не имеет ни максимума, ни минимума при . При этом

убывает, если

возрастает, если .

Пример. , найти максимум, минимум.

1. Критические точки

, порядок чётный и минимум .

Выпуклость и вогнутость кривой. Точки перегиба.

Рассмотри кривую , которая является графиком однозначной, дифференцируемой функции .

Определение 1. Будем говорить, что кривая обращена выпуклостью вверх на интервале , если все точки кривой лежат ниже любой касательной, проведенной к любой точке из этого интервала.

Кривая обращена выпуклостью вниз на интервале , если все её точки лежат выше любой её касательной на .

Кривая, обращённая выпуклостью вверх, называется выпуклой, а обращённая выпуклостью вниз – вогнутой.

В этом разделе мы установим признаки, которые позволяют судить о направлении выпуклости графика на различных интервалах определения .

Теорема 1. Если кривая выпукла на .

Доказательство. Пусть . Проведём касательную к графику в точке с абсциссой . Теорема будет доказана, если все точки будут лежать ниже этой касательной. Т.е. ордината будет меньше ординаты у касательной при одном и том же значении .

Как установлено ранее, уравнение касательной в точке имеет вид:

или

.

Нас интересует знак разности , которую можно записать в виде:

.

Применяя т. Лагранжа к разности 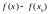мы можем записать:

(где С лежит между и ), или

,

и к разности производных опять применим ту же теорему

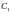, между и .

Рассмотрим теперь случай . Тогда ; т.к. и и по условию теоремы , т.е. Теорема 1 доказана.

Пусть теперь , тогда . В этом случае 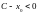и , но .

Таким образом мы доказали, что и ордината касательной больше ординаты графика , а это означает, что кривая выпукла, Теорема 1 доказана.

Аналогично доказывается и Теорема 1’.

Теорема 1’. Если , то кривая вогнута на .

Геометрическая интерпретация.

есть - угла наклона касательной в точке с абсциссой . Поэтому Если убывает при возрастании .

Если же возрастает при возрастании .

Пример: установить интервалы выпуклости и вогнутости кривой.

- кривая выпукла.

- кривая вогнута.

Определение 2. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба этой кривой.

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой – над нею.

Сформулируем теперь достаточные условия того, что данная точка является точкой перегиба.

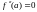Теорема 2. Пусть кривая определяется уравнением . Если , или не существует, и при переходе через меняет знак, то точка кривой с есть точка перегиба.

Доказательство. 1) при и

при .

Тогда, при кривая выпукла, а при - вогнута. Следовательно, есть точка перегиба.

2. Пусть теперь при и при , тогда при кривая вогнута, а при - выпукла. Следовательно, точка есть точка перегиба.

Пример.

(кривая Гаусса)

- нет точек перегиба

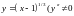, но при не существует

Асимптоты.

Довольно часто требуется исследовать форму кривой при неограниченном возрастании . Важным частным случаем является тот, когда исследуемая кривая при удалении её переменной точки в бесконечность (т.е. при расстояния от начала координат до этой точки) неограниченно приближается к некоторой прямой.

Определение. Прямая А называется асимптотой кривой, если расстояние от точки до этой прямой стремится к нулю.

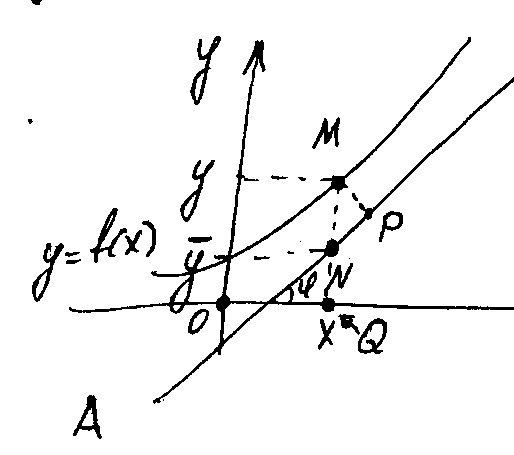
Различают вертикальные асимптоты – т.е. параллельные OY, горизонтальные – т.е. параллельные OX и наклонные, т.е. не параллельные OY или OX.

1. Вертикальные асимптоты. Из определения следует, что если

,

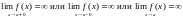то прямая есть асимптота кривой , и обратно, что если есть асимптота, то выполняется одно из написанных равенств.

Следовательно, для нахождения вертикальных асимптот нужно найти такие , чтобы при 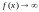. Тогда и будет асимптотой.

Пример. , - асимптота, т.к. , .

- б.м. вертикальных асимптот, ,

т.к. при .

2. Наклонные асимптоты. Пусть имеет наклонную асимптоту

1. .

Определим коэффициенты и . Пусть и . расстояние от до . По условию

2. 

Пусть - угол наклона к оси из ; т.к. , то

(2’) .

При этом из (2) (2’) и наоборот. С другой стороны, и (2’) приобретает вид:

3. .

Итак, если (1) есть асимптота, то выполняется (3) и, наоборот, если выполняется (3), то (1) – уравнение асимптоты.

Определим теперь и . Вынося за скобки, получим

Т.к. 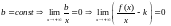или

Зная теперь можно найти и из (3)

Итак, если есть асимптота, (*)

Обратное также справедливо. Если существуют пределы (*), то есть асимптота. Если же хотя бы один из пределов не существует, то асимптоты не имеет. Пример.

1. Найдём вертикальные асимптоты:

- вертикальная асимптота.

2. Ищем наклонные асимптоты:

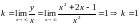
- асимптота.

Пример. , вертикальных нет,

при ,при асимптоты нет.