
- •Функция. Основные определения и понятия.
- •График функции
- •1. Функция
- •Сложная функция.
- •Обратная функция.
- •Основные элементарные функции.
- •Четные и нечётные функции.
- •Периодические функции.
- •Ограниченные функции.
- •Монотонные функции. Экстремум функции.
- •Бесконечно малые и бесконечно большие величины
- •4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними
- •Связь бесконечно малой и бесконечно большой величины
- •Сравнение бесконечно малых Определения
- •Примеры сравнения
- •Эквивалентные величины Определение
- •Предел числовой последовательности.
- •Предел последовательности
- •Основные свойства пределов
- •5.4. Предел функции
- •Односторонний предел по Гейне
- •Односторонний предел по Коши
- •Односторонний предел как предел вдоль фильтра
- •Обозначения
- •Свойства
- •6.2. Свойства функций, непрерывных в точке
- •6.3. Свойства функций, непрерывных на отрезке
- •Графики дробно-линейной и дробно-рациональной функций
- •Первый и второй замечательные пределы
- •6.1. Непрерывность функции в точке
- •Определение производной
- •Составим отношение
- •Геометрический смысл производной
- •Непрерывность и дифференцируемость функций
- •Правила дифференцирования
- •Доказательство. Итак
- •Дифференцирование неявных функций и заданных параметрических
- •Дифференциал функции
- •Дифференциал сложной функции равен производной этой функции по
- •Формула Лейбница
- •Доказательство.
- •Исследование функции на экстремум с помощью второй роизводной.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Формула Тейлора
- •Разложение по формуле Тейлора функций
- •Исследование функции на максимум и минимум с помощью формулы Тейлора.
- •Выпуклость и вогнутость кривой. Точки перегиба.
- •Исследование кривых,заданных параметрами. Пусть , исследуем ан. Вычисляем и .Для точек кривой, вблизи которых кривая является графиком некоторой функции , вычисляем .
- •Общий план исследования функций и построения графиков.
- •Элементы дифференциальной геометрии.Касательная и нормаль к плоской кривой.
- •Дифференциал дуги плоской и пространственной кривой.
- •Кривизна плоской кривой.
- •Векторная функция скалярного аргументаи её дифференцирование.
- •Приближённое решение уравнений.Интерполирование функций. Действительные корни .
- •Методы уточнения приближённого корня.
- •Интерполяционные формулы Лагранжа и Ньютона.
- •Интерполирующая функция Лагранжа.
Исследование функции на экстремум с помощью второй роизводной.
Пусть
при
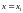 производная от
производная от
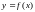 обращается в нуль, т.е.
обращается в нуль, т.е.
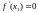 .
Пусть, кроме того,
.
Пусть, кроме того,
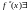 и непрерывна в окрестности
и непрерывна в окрестности
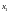 .
Тогда справедлива
.
Тогда справедлива
Теорема.
Пусть
,
тогда при
 имеет максимум, если
имеет максимум, если
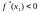 и минимум, если
и минимум, если
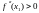 .
.
Доказательство.
Пусть
и
.
Т.к.
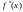 непрерывна, то
непрерывна, то
 малый отрезок, содержащий
,
во всех точках которого
малый отрезок, содержащий
,
во всех точках которого
 .
.
Т.к.
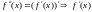 убывает на выбранном отрезке
убывает на выбранном отрезке
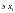 .
Но
.
Но
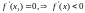 ,
при
,
при
 и
и
 при
при
 .
Т.е. при переходе через
.
Т.е. при переходе через
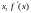 меняет знак с “+” на “-“, а это значит,
что
меняет знак с “+” на “-“, а это значит,
что
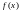 имеет в
имеет в
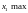 .
.
Пусть
теперь
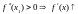 в
окрестности
.
Т.к.
в
окрестности
.
Т.к.
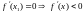 при
и
при
.
Т.о., при переходе через
при
и
при
.
Т.о., при переходе через
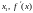 изменяет знак с “-” на “+“, т.о. мы имеем
в
изменяет знак с “-” на “+“, т.о. мы имеем
в
 .
.
Если
в
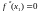 ,
то в этой точке может быть max,
min,
или не быть ни того ни другого. В этом
случае исследование функции надо вести
первым способом (т.е. исследовать знак
первой производной).
,
то в этой точке может быть max,
min,
или не быть ни того ни другого. В этом
случае исследование функции надо вести
первым способом (т.е. исследовать знак
первой производной).
Схема исследования.
-
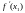
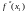
Крит. точка
0
<0, “ – “
max
0
>0, “+”
min
0
0
неизвестно
П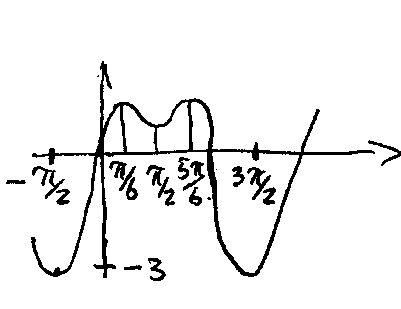 ример:
ример:
Наибольшее и наименьшее значения функции на отрезке.
Пусть непрерывна на [a, b]. Тогда она достигает на нём своего наибольшего и наименьшего значений.
Предположим,
что
имеет на [a,
b]
конечное число критических точек. Если
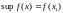 ,
где
,
где
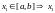 -
точка max
(одного из), точнее – наибольший max.
Однако может случиться, что sup
достигается на одном из концов отрезка.
-
точка max
(одного из), точнее – наибольший max.
Однако может случиться, что sup
достигается на одном из концов отрезка.
Итак,
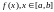 достигает sup
либо в одной из точек max,
либо на концах отрезка.
достигает sup
либо в одной из точек max,
либо на концах отрезка.
То же самое можно сказать и о наименьшем значении : оно достигается либо на конце (концах) отрезка, либо во внутренней точке, является точкой min.
Итак, если требуется найти наибольшее (наименьшее) значение непрерывной , то необходимо:
Найти все max (min) на отрезке [a, b]
Вычислить значения при

Из всех полученных выше значений выбрать наибольшее (наименьшее).
Пример.
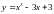 .
Найти supr
и inf
на
.
Найти supr
и inf
на
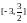
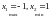
Формула Тейлора
Предположим,
что
имеет все произвольные до n+1
–го порядка включительно в окрестности
 .
Найдём многочлен
.
Найдём многочлен
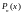 степени не выше n,
такой, что
степени не выше n,
такой, что
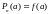 ,
а
,
а
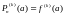 ,
где
,
где
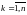 :
Итак
:
Итак
(1)
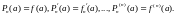
Естественно
предположить, то
 «близок» к
в некотором смысле.
«близок» к
в некотором смысле.
Будем
искать
в форме многочлена по степеням
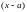 с неопределёнными коэффициентами:
с неопределёнными коэффициентами:
(2)
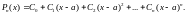
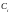 будем
искать из условия (1). Предварительно
найдём производные от
будем
искать из условия (1). Предварительно
найдём производные от
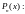
(3)
Подставляя
теперь вместо
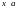 и заменяя
и заменяя
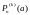 на
на
 ,
согласно (1), получим:
,
согласно (1), получим:
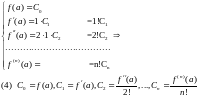
Подставляя
теперь вместо
в
 получим
получим
(5)
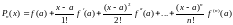
Обозначим
теперь через
 разность между
:
разность между
:
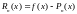 и
тогда
и
тогда
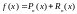 или в развёрнутом виде
или в развёрнутом виде
(6)
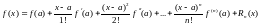
называют
остаточным членом. Для тех значений
 ,
для которых
мал,
даёт приближённое представление
.
,
для которых
мал,
даёт приближённое представление
.
Т.о. (6) даёт возможность заменить многочленом с точностью, определяемой .
Следующая задача – оценить при различных . Запишем в форме
 ,
,
где
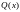 -
некоторая функция, которую нужно
определить. При фиксированных
и
-
некоторая функция, которую нужно
определить. При фиксированных
и
 имеет определённое значение
имеет определённое значение
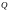 .
.
Рассмотрим
далее вспомогательную функцию от

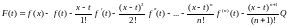
Далее
найдём
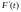

После сокращения получим
(*)
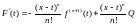
Итак,
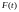 имеет производную для
имеет производную для
 ,
причём
,
причём
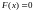 и
и
 .
Поэтому к
применима т. Ролля:
.
Поэтому к
применима т. Ролля:
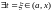 ,
в которой
,
в которой
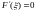 .
Отсюда и из (*) следует, что
.
Отсюда и из (*) следует, что
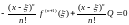 или
или
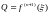 и тогда
и тогда
остаточный
член в форме Лагранжа. Т.к.
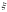 заключено между
и
,
то его можно представить в виде
заключено между
и
,
то его можно представить в виде
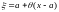 ,
где
,
где
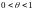 ,
и тогда
,
и тогда
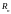 можно записать в виде:
можно записать в виде:

Формула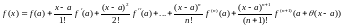 называется формулой Тейлора для
.
называется формулой Тейлора для
.
Если
в формуле Тейлора положить
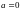 ,
то
,
то
(**)
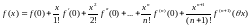 .
.
Этот частный случай формулы Тейлора называют формулой Маклорена.
