
- •Функция. Основные определения и понятия.
- •График функции
- •1. Функция
- •Сложная функция.
- •Обратная функция.
- •Основные элементарные функции.
- •Четные и нечётные функции.
- •Периодические функции.
- •Ограниченные функции.
- •Монотонные функции. Экстремум функции.
- •Бесконечно малые и бесконечно большие величины
- •4.6. Свойства бесконечно малых и бесконечно больших величин и связь между ними
- •Связь бесконечно малой и бесконечно большой величины
- •Сравнение бесконечно малых Определения
- •Примеры сравнения
- •Эквивалентные величины Определение
- •Предел числовой последовательности.
- •Предел последовательности
- •Основные свойства пределов
- •5.4. Предел функции
- •Односторонний предел по Гейне
- •Односторонний предел по Коши
- •Односторонний предел как предел вдоль фильтра
- •Обозначения
- •Свойства
- •6.2. Свойства функций, непрерывных в точке
- •6.3. Свойства функций, непрерывных на отрезке
- •Графики дробно-линейной и дробно-рациональной функций
- •Первый и второй замечательные пределы
- •6.1. Непрерывность функции в точке
- •Определение производной
- •Составим отношение
- •Геометрический смысл производной
- •Непрерывность и дифференцируемость функций
- •Правила дифференцирования
- •Доказательство. Итак
- •Дифференцирование неявных функций и заданных параметрических
- •Дифференциал функции
- •Дифференциал сложной функции равен производной этой функции по
- •Формула Лейбница
- •Доказательство.
- •Исследование функции на экстремум с помощью второй роизводной.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Формула Тейлора
- •Разложение по формуле Тейлора функций
- •Исследование функции на максимум и минимум с помощью формулы Тейлора.
- •Выпуклость и вогнутость кривой. Точки перегиба.
- •Исследование кривых,заданных параметрами. Пусть , исследуем ан. Вычисляем и .Для точек кривой, вблизи которых кривая является графиком некоторой функции , вычисляем .
- •Общий план исследования функций и построения графиков.
- •Элементы дифференциальной геометрии.Касательная и нормаль к плоской кривой.
- •Дифференциал дуги плоской и пространственной кривой.
- •Кривизна плоской кривой.
- •Векторная функция скалярного аргументаи её дифференцирование.
- •Приближённое решение уравнений.Интерполирование функций. Действительные корни .
- •Методы уточнения приближённого корня.
- •Интерполяционные формулы Лагранжа и Ньютона.
- •Интерполирующая функция Лагранжа.
Первый и второй замечательные пределы
 Определение
2 . 11 Первым замечательным пределом
называется предел
Определение
2 . 11 Первым замечательным пределом
называется предел
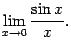 Теорема 2 . 14
Первый замечательный предел равен
Теорема 2 . 14
Первый замечательный предел равен
![]()
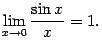 Доказательство
. Рассмотрим
два односторонних предела
Доказательство
. Рассмотрим
два односторонних предела
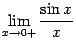 и
и
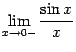 и
докажем, что каждый из них равен 1. Тогда
по теореме 2.1 двусторонний предел
и
докажем, что каждый из них равен 1. Тогда
по теореме 2.1 двусторонний предел
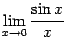 также
будет равняться 1. Итак, пусть
также
будет равняться 1. Итак, пусть
![]() (этот
интервал -- одно из окончаний базы
(этот
интервал -- одно из окончаний базы
![]() ).
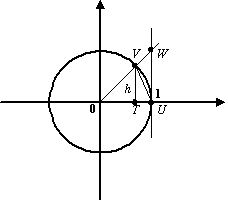
В тригонометрическом круге (радиуса
).
В тригонометрическом круге (радиуса
![]() )
с центром
)
с центром
![]() построим
центральный угол, равный
построим
центральный угол, равный
![]() ,
и проведём вертикальную касательную в
точке
,
и проведём вертикальную касательную в
точке
![]() пересечения
горизонтальной оси с окружностью (
пересечения
горизонтальной оси с окружностью (
![]() ).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой
).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой
![]() ,
а с вертикальной касательной -- буквой
,
а с вертикальной касательной -- буквой
![]() ;
через
;
через
![]() обозначим
проекцию точки
на
горизонтальную ось. Рис. 2 . 27
.Тригонометрический круг Пусть
обозначим
проекцию точки
на
горизонтальную ось. Рис. 2 . 27
.Тригонометрический круг Пусть
![]() --
площадь треугольника
--
площадь треугольника
![]() ,
,
![]() --
площадь кругового сектора
,
а
--
площадь кругового сектора
,
а
![]() --
площадь треугольника
--
площадь треугольника
![]() .
Тогда очевидно следующее неравенство:
.
Тогда очевидно следующее неравенство:
![]() Заметим,
что горизонтальная координата точки
равна
Заметим,
что горизонтальная координата точки
равна
![]() ,
а вертикальная --
,
а вертикальная --
![]() (это
высота треугольника
),
так что
(это
высота треугольника
),
так что
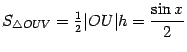 .
Площадь центрального сектора круга
радиуса
.
Площадь центрального сектора круга
радиуса
![]() с
центральным углом
равна
с
центральным углом
равна
![]() ,
так что
,
так что
![]() .
Из треугольника
находим,
что
.
Из треугольника
находим,
что
![]() .
Поэтому
.
Поэтому
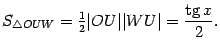 Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
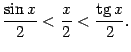 Все
три части этого неравенства положительны,
поэтому его можно записать так:
Все
три части этого неравенства положительны,
поэтому его можно записать так:
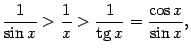 или
(умножив на
или
(умножив на
![]() )
так:
)
так:
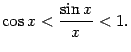 Предел
постоянной 1 в правой части неравенства,
очевидно, равен 1. Если мы покажем, что
при
предел
Предел
постоянной 1 в правой части неравенства,
очевидно, равен 1. Если мы покажем, что
при
предел
![]() в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части
в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части
![]() также
будет равен 1. Итак, осталось доказать,
что
также
будет равен 1. Итак, осталось доказать,
что
![]() .
Сперва заметим, что
.
Сперва заметим, что
![]() ,
так как
равняется
длине дуги окружности
,
так как
равняется
длине дуги окружности
![]() ,
которая, очевидно, длиннее хорды
,
которая, очевидно, длиннее хорды
![]() .
Применяя теорему "о двух милиционерах"
к неравенству
.
Применяя теорему "о двух милиционерах"
к неравенству
![]() при
,
получаем, что
при
,
получаем, что
![]() (
2 .3) Простая замена переменной
(
2 .3) Простая замена переменной
![]() показывает,
что и
показывает,
что и
![]() .
Теперь заметим, что
.
Теперь заметим, что
![]() .
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
.
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
![]() (
2 .4) Тем самым показано, что
(
2 .4) Тем самым показано, что
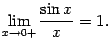 Сделаем
теперь замену
Сделаем
теперь замену
![]() ;
при этом база
перейдёт
в базу
;
при этом база
перейдёт
в базу
![]() (что
означает, что если
(что
означает, что если
![]() ,
то
,
то
![]() ).
Значит,
).
Значит,
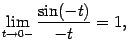 но
но
![]() (
(
![]() --
нечётная функция), и поэтому
--
нечётная функция), и поэтому
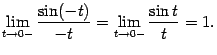 Мы
показали, что левосторонний предел
также равен 1, что и завершает доказательство
теоремы. Доказанная теорема
означает, что график функции
Мы
показали, что левосторонний предел
также равен 1, что и завершает доказательство
теоремы. Доказанная теорема
означает, что график функции
 выглядит
так:
выглядит
так:
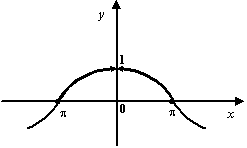 Рис.
2 . 28 .График
Рис.
2 . 28 .График
Определение
2 . 12 Вторым
замечательным пределом называется
предел
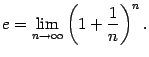 Число
Число
![]() ,
заданное этим пределом, играет очень
большую роль как в математическом
анализе, так и в других разделах
математики. Число
часто
называют основанием натуральных
логарифмов . Теорема
2 . 15 Второй замечательный предел
существует. Его значение
--
число, лежащее между
,
заданное этим пределом, играет очень
большую роль как в математическом
анализе, так и в других разделах
математики. Число
часто
называют основанием натуральных
логарифмов . Теорема
2 . 15 Второй замечательный предел
существует. Его значение
--
число, лежащее между
![]() и
и
![]() .
Более подробное изучение числа
показывает,
что
--
иррациональное число, несколько первых
десятичных знаков которого таковы:
.
Более подробное изучение числа
показывает,
что
--
иррациональное число, несколько первых
десятичных знаков которого таковы:
![]() Для
доказательства теоремы 2.15 нам понадобится
следующая лемма; формула, в ней полученная,
называется формулой бинома Ньютона .
Лемма 2 . 2
Пусть
Для
доказательства теоремы 2.15 нам понадобится
следующая лемма; формула, в ней полученная,
называется формулой бинома Ньютона .
Лемма 2 . 2
Пусть
![]() и
и
![]() --
натуральное число. Тогда имеет место
формула
--
натуральное число. Тогда имеет место
формула
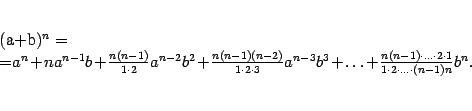 Заметим,
что в дроби
Заметим,
что в дроби
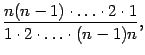 очевидно,
сокращаются все сомножители в числителе
и знаменателе, так что эта дробь равна
1. Аналогично, в предыдущем (не выписанном)
слагаемом после сокращения получается
коэффициент, равный
,
в третьем справа слагаемом -- равный
очевидно,
сокращаются все сомножители в числителе
и знаменателе, так что эта дробь равна
1. Аналогично, в предыдущем (не выписанном)
слагаемом после сокращения получается
коэффициент, равный
,
в третьем справа слагаемом -- равный
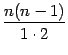 ,
и т. д. Таким образом, коэффициенты
в слагаемых, стоящих на одинаковых
местах, считая слева и справа от края
формулы, совпадают.
Доказательство . Доказывать
утверждение леммы будем по индукции по
параметру
.
При
,
и т. д. Таким образом, коэффициенты
в слагаемых, стоящих на одинаковых
местах, считая слева и справа от края
формулы, совпадают.
Доказательство . Доказывать
утверждение леммы будем по индукции по
параметру
.
При
![]() формула
2.2 , очевидно, верна:
формула
2.2 , очевидно, верна:
![]() (Заметим,
что при
(Заметим,
что при
![]() и
и
![]() формула
2.2 также хорошо известна:
формула
2.2 также хорошо известна:
![]() и
и
![]() Предположим,
что она верна для
Предположим,
что она верна для
![]() ,
и докажем, что тогда она верна и при
,
и докажем, что тогда она верна и при
![]() .
Действительно,
.
Действительно,
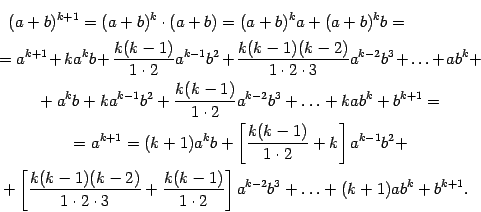 При
этом в квадратных скобках получается:
При
этом в квадратных скобках получается:
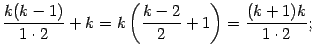
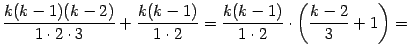
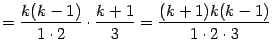 и так далее, то есть как раз то, что должно
получиться в качестве коэффициентов
формулы бинома Ньютона при
.
Доказательство теоремы 2.15 .
Рассмотрим последовательность
и так далее, то есть как раз то, что должно
получиться в качестве коэффициентов
формулы бинома Ньютона при
.
Доказательство теоремы 2.15 .
Рассмотрим последовательность
![]() и
применим к
и
применим к
![]() формулу
бинома Ньютона при
формулу
бинома Ньютона при
![]() и
и
![]() .
Получим
.
Получим
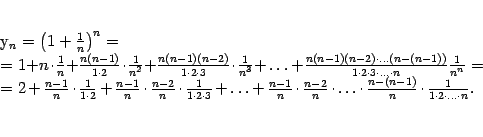 Покажем,
что последовательность
ограничена
сверху. Для этого заменим все дроби
Покажем,
что последовательность
ограничена
сверху. Для этого заменим все дроби
![]() ,
,
![]() ,
...,
,
...,
![]() на
1. Все эти дроби меньше 1, так что сумма
в правой части формулы ( Доказательство
теоремы 2.15 ) увеличится:
на
1. Все эти дроби меньше 1, так что сумма
в правой части формулы ( Доказательство
теоремы 2.15 ) увеличится:
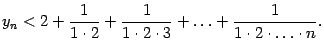 Далее,
заменим все числа
Далее,
заменим все числа
![]() в
знаменателях этих слагаемых на 2; от
этого правая часть ещё увеличится.
Получим:
в
знаменателях этих слагаемых на 2; от
этого правая часть ещё увеличится.
Получим:
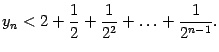 В
правой части получилась сумма членов
геометрической прогрессии. Она равна
В
правой части получилась сумма членов
геометрической прогрессии. Она равна
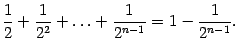 Поэтому
Поэтому
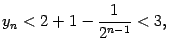 что
и означает ограниченность последовательности
сверху числом 3. Покажем теперь, что
последовательность
не
убывает. Действительно, запишем формулу
( Доказательство теоремы 2.15 ) в виде
что
и означает ограниченность последовательности
сверху числом 3. Покажем теперь, что
последовательность
не
убывает. Действительно, запишем формулу
( Доказательство теоремы 2.15 ) в виде
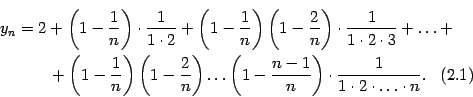 В
аналогичной формуле, написанной для
В
аналогичной формуле, написанной для
![]() вместо
,
во-первых, увеличится каждое из выражений
в круглых скобках (так как вычитаемое
уменьшится) и, значит, увеличатся все
слагаемые, содержащие такие скобки.
Во-вторых, число слагаемых увеличится
на одно: добавится положительное
слагаемое
вместо
,
во-первых, увеличится каждое из выражений
в круглых скобках (так как вычитаемое
уменьшится) и, значит, увеличатся все
слагаемые, содержащие такие скобки.
Во-вторых, число слагаемых увеличится
на одно: добавится положительное
слагаемое
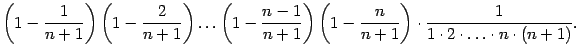 Следовательно,
при росте номера
члены
последовательности
строго
возрастают:
Следовательно,
при росте номера
члены
последовательности
строго
возрастают:
![]() при
всех
при
всех
![]() .
Применим теперь к возрастающей
ограниченной сверху последовательности
теорему
о пределе монотонной ограниченной
функции ( теорема 2.13 ) и получим, что
существует предел
.
Применим теперь к возрастающей
ограниченной сверху последовательности
теорему
о пределе монотонной ограниченной
функции ( теорема 2.13 ) и получим, что
существует предел
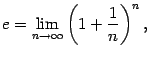 причём
число
не
больше постоянной 3, ограничивающей
последовательность. Осталось заметить,
что
причём
число
не
больше постоянной 3, ограничивающей
последовательность. Осталось заметить,
что
![]() .
Так как все последующие члены
ещё
больше, то и предел
,
на основании теоремы о переходе к пределу
в неравенстве ( следствие 2.7 ), не меньше
числа
.
Так как все последующие члены
ещё
больше, то и предел
,
на основании теоремы о переходе к пределу
в неравенстве ( следствие 2.7 ), не меньше
числа
![]() ,
что и завершает доказательство теоремы.
Замечание
2 . 7 Можно также показать, что
,
что и завершает доказательство теоремы.
Замечание
2 . 7 Можно также показать, что
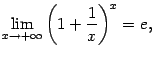 (
2 .5) однако строгое доказательство
достаточно тяжело, и мы его здесь
пропускаем. В формуле ( 2.5 ) можно сделать
замену
(
2 .5) однако строгое доказательство
достаточно тяжело, и мы его здесь
пропускаем. В формуле ( 2.5 ) можно сделать
замену
![]() ,
при этом база
,
при этом база
![]() перейдёт
в базу
перейдёт
в базу
![]() ,
и мы получим
,
и мы получим
![]() Упражнение
2 . 6 Покажите, что имеют место также
равенства
Упражнение
2 . 6 Покажите, что имеют место также
равенства
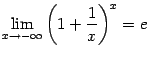 и
и
![]() На
этой основе, применяя теоремы о связи
двусторонних пределов с односторонними,
покажите, что
На
этой основе, применяя теоремы о связи
двусторонних пределов с односторонними,
покажите, что
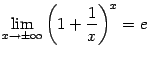 и
и
![]() Формулы в этих замечании и упражнении
представляют собою другую форму записи
второго замечательного предела. Мы
сохраним название второй замечательный
предел за всеми этими формулами.
Пример 2 . 22
Найдём предел
Формулы в этих замечании и упражнении
представляют собою другую форму записи
второго замечательного предела. Мы
сохраним название второй замечательный
предел за всеми этими формулами.
Пример 2 . 22
Найдём предел
![]() .
Здесь параметр
.
Здесь параметр
![]() --
фиксированное число. При вычислении
предела он будет рассматриваться как
постоянная. Сделаем замену
--
фиксированное число. При вычислении
предела он будет рассматриваться как
постоянная. Сделаем замену
![]() ,
тогда
,
тогда
![]() и
и
![]() .
Поэтому
.
Поэтому
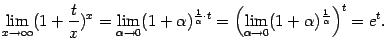 (Здесь
мы воспользовались, пока на интуитивном
уровне, тем, что степенная функция
непрерывна, то есть что
(Здесь
мы воспользовались, пока на интуитивном
уровне, тем, что степенная функция
непрерывна, то есть что
![]() .
Более подробно понятие непрерывности
функций мы будем изучать ниже, в разделе
Использование непрерывности функций
при вычислении пределов .) Полученная
формула даёт нам возможность выразить
экспоненциальную функцию
.
Более подробно понятие непрерывности
функций мы будем изучать ниже, в разделе
Использование непрерывности функций
при вычислении пределов .) Полученная
формула даёт нам возможность выразить
экспоненциальную функцию
![]() как
некоторый предел. С помощью
похожей замены вычисляются пределы
функций вида
как
некоторый предел. С помощью
похожей замены вычисляются пределы
функций вида
![]() в
случае, когда основание степени
в
случае, когда основание степени
![]() при
некоторой базе стремится к 1, а показатель
степени
при
некоторой базе стремится к 1, а показатель
степени
![]() --
к бесконечности (то есть является
бесконечно большой функцией при данной
базе; о бесконечно больших см. ниже,
в разделе Бесконечно большие величины
и бесконечные пределы ). Такие выражения,
а также и связанные с ними пределы,
называются неопределённостями вида
--
к бесконечности (то есть является
бесконечно большой функцией при данной
базе; о бесконечно больших см. ниже,
в разделе Бесконечно большие величины
и бесконечные пределы ). Такие выражения,
а также и связанные с ними пределы,
называются неопределённостями вида
![]() .
О неопределённостях других видов пойдёт
речь ниже, после примера 2.29 . Обратим
внимание читателя, что
--
это лишь условная запись: 1 здесь
указывает, что основание степени
стремится к 1 (и вовсе не обязательно
равно 1 ); в "показателе степени"
стоит вообще не число, а символ
бесконечности. Поэтому было бы грубой
ошибкой, встретив такую условную запись
(или написав её), сделать вывод о том,
что единица, мол, в любой степени даёт
единицу, и поэтому ответ равен единице.
С условными символами в этой записи
нельзя действовать так же, как с числами.
Предыдущий пример, в котором основание
степени
.
О неопределённостях других видов пойдёт
речь ниже, после примера 2.29 . Обратим
внимание читателя, что
--
это лишь условная запись: 1 здесь
указывает, что основание степени
стремится к 1 (и вовсе не обязательно
равно 1 ); в "показателе степени"
стоит вообще не число, а символ
бесконечности. Поэтому было бы грубой
ошибкой, встретив такую условную запись
(или написав её), сделать вывод о том,
что единица, мол, в любой степени даёт
единицу, и поэтому ответ равен единице.
С условными символами в этой записи
нельзя действовать так же, как с числами.
Предыдущий пример, в котором основание
степени
![]() стремится
к 1, а показатель степени
к
стремится
к 1, а показатель степени
к
![]() ,
даёт как раз неопределённость вида
.
Однако значение предела равно
,
а этот результат может быть любым
положительным числом , в зависимости
от того, какое значение
,
даёт как раз неопределённость вида
.
Однако значение предела равно
,
а этот результат может быть любым
положительным числом , в зависимости
от того, какое значение
![]() взято.
Вот ещё один пример на раскрытие
неопределённости вида
.
Пример 2 . 23
Найдём предел
взято.
Вот ещё один пример на раскрытие
неопределённости вида
.
Пример 2 . 23
Найдём предел
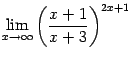 .
Здесь основание степени имеет предел
.
Здесь основание степени имеет предел
 а
показатель степени
а
показатель степени
![]() .
Поэтому можно применять тот же приём
сведения ко второму замечательному
пределу, что в предыдущем примере. Для
начала найдём, что следует взять за
бесконечно малую величину
.
Поэтому можно применять тот же приём
сведения ко второму замечательному
пределу, что в предыдущем примере. Для
начала найдём, что следует взять за
бесконечно малую величину
![]() .
Поскольку основание степени стремится
к 1, то оно равно
.
Поскольку основание степени стремится
к 1, то оно равно
![]() ,
где
,
где
![]() (см.
теорему 2.4 ). Значит,
(см.
теорему 2.4 ). Значит,
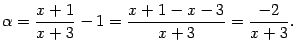 Теперь
преобразуем функцию, стоящую под знаком
предела:
Теперь
преобразуем функцию, стоящую под знаком
предела:
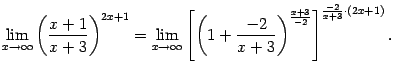 Выражение,
стоящее в квадратных скобках, имеет вид
Выражение,
стоящее в квадратных скобках, имеет вид
![]() и
при
стремится
к числу
(это
второй замечательный предел), а предел
показателя степени мы найдём отдельно:
и
при
стремится
к числу
(это
второй замечательный предел), а предел
показателя степени мы найдём отдельно:
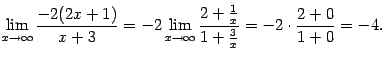 Поэтому
Поэтому
 (Мы
воспользовались тем, что если
(Мы
воспользовались тем, что если
![]() и
и
![]() ,
то
,
то
![]() .
Это следует из непрерывности показательной
и логарифмической функций, если учесть,
что
.
Это следует из непрерывности показательной
и логарифмической функций, если учесть,
что
![]() .)
Замечание
2 . 8 Не любые пределы величин вида
вычисляются
с помощью сведения ко второму замечательному
пределу. Ещё раз напомним, что так надо
поступать лишь в случае, когда основание
степени
при
данной базе стремится к 1, а показатель
степени
--
к бесконечности. В иных ситуациях можно
бывает для вычисления предела обойтись
более простыми рассуждениями. Например,
при нахождении предела
.)
Замечание
2 . 8 Не любые пределы величин вида
вычисляются
с помощью сведения ко второму замечательному
пределу. Ещё раз напомним, что так надо
поступать лишь в случае, когда основание
степени
при
данной базе стремится к 1, а показатель
степени
--
к бесконечности. В иных ситуациях можно
бывает для вычисления предела обойтись
более простыми рассуждениями. Например,
при нахождении предела
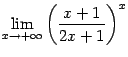 можно
заметить, что основание степени стремится
к
можно
заметить, что основание степени стремится
к
![]() ,
так что получается формально
,
так что получается формально
![]() .
Это выражение не является неопределённостью
(в отличие от выражения
),
так как основание степени при достаточно
больших
близко
к
(и
заведомо меньше, скажем,
.
Это выражение не является неопределённостью
(в отличие от выражения
),
так как основание степени при достаточно
больших
близко
к
(и
заведомо меньше, скажем,
![]() )
и при возведении в неограниченно
увеличивающуюся степень
будет
меньше
)
и при возведении в неограниченно
увеличивающуюся степень
будет
меньше
![]() и,
следовательно, будет стремиться к 0. Так
что
и,
следовательно, будет стремиться к 0. Так
что
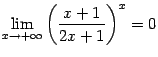
Непрерывность
функций.
Рассмотрим функцию
определённую в некоторой точке
 и некоторой окрестности точки
.
Пусть в указанной точке функция имеет
значение
и некоторой окрестности точки
.
Пусть в указанной точке функция имеет
значение
 .
.
Определение
1. Функция
называется
непрерывной в точке
,
если она определена в окрестности точки
, включая саму точку и
 .
.
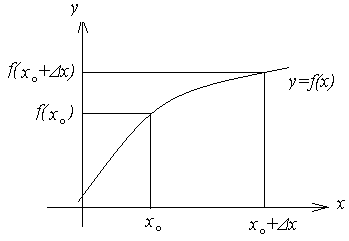 Определение
непрерывности можно сформулировать
иначе
Определение
непрерывности можно сформулировать
иначе
Пусть
функция
определена при некотором значении
,
 .
Если аргументу
дать приращение
.
Если аргументу
дать приращение
 ,
то функция получит приращение
,
то функция получит приращение

 .
.
Пусть функция в точке непрерывна (по первому определению непрерывности функции в точке),
тогда

или
 .
.
То есть, если функция непрерывна в точке , то бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции.
Справедливо и обратное предложение: если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция непрерывна.
Определение
2. Функция
называется непрерывной при
 (в точке
),
если она определена в этой точке и
некоторой её окрестности и если
(в точке
),
если она определена в этой точке и
некоторой её окрестности и если
 .
.
Учитывая первое и второе определение непрерывности функции в точке можно получить следующее утверждение:

или
,
но
 ,
тогда
,
тогда
 .
.
Следовательно,
для того чтобы найти предел непрерывной
функции при
 достаточно в аналитическое выражение
функции вместо аргумента
подставить его значение
.
достаточно в аналитическое выражение
функции вместо аргумента
подставить его значение
.
Определение 3. Функция, непрерывная в каждой точке некоторой области называется непрерывной в этой области.
Например:
Пример
1. Доказать, что функция
 непрерывна во всех точках области
определения.
непрерывна во всех точках области
определения.
Воспользуемся вторым определением непрерывности функции в точке. Для этого возьмём любое значение аргумента и дадим ему приращение . Найдём соответствующее приращение функции

Тогда
 ;
;
Определение
4. Если функция
непрерывна в каждой точке некоторого
интервала
 ,
то говорят, что функция непрерывна на
этом интервале.
,
то говорят, что функция непрерывна на
этом интервале.
Теорема
1. Если две
функции
и
 непрерывны в точке
,
то функции
непрерывны в точке
,
то функции
 также непрерывны в точке
.
также непрерывны в точке
.
Доказательство:
Так
как
и
непрерывны в точке
,
то
и
 .
.
Воспользуемся теоремами о пределах функции

Теорема доказана.
Теорема
2. Если
функция
непрерывна на отрезке
 ,
то на этом отрезке найдётся по крайней
мере одна точка
,
то на этом отрезке найдётся по крайней
мере одна точка
 такая, что значение функции в этой точке
такая, что значение функции в этой точке
 будет больше, чем значение функции в
любой точке этого отрезка, т.е.
будет больше, чем значение функции в
любой точке этого отрезка, т.е.
 ;
и найдётся по крайней мере одна точка
;
и найдётся по крайней мере одна точка
 такая, что значение функции в этой точке
такая, что значение функции в этой точке
 будет
меньше, чем значение функции в любой
точке этого отрезка, т.е.
будет
меньше, чем значение функции в любой
точке этого отрезка, т.е.
 .
.
Значение функции называется наибольшим значением функции на отрезке, значение функции называется наименьшим значением функции на отрезке.
Теорема
3. Если
функция
непрерывна на отрезке
и на концах отрезка принимает значения
разных знаков, то внутри отрезка
найдётся по крайней мере одна точка, в
которой
 .
.
Теорема
4. Если
функция
непрерывна на отрезке
и на концах отрезка принимает неравные
между собой значения
 и
и
 ,
то каково бы ни было число
,
то каково бы ни было число
 внутри отрезка
внутри отрезка
 ,
такое что
,
такое что
 ,
найдётся по крайней мере одна точка
,
найдётся по крайней мере одна точка
 ,
в которой функция принимает значение
равное
,
т.е.
,
в которой функция принимает значение
равное
,
т.е.
 .
.
Если
в какой-нибудь точке
 нарушается условие непрерывности (т.е.
либо
нарушается условие непрерывности (т.е.
либо
 ,
либо
,
либо
 ,
либо не определена в ), то говорят, что
функция в точке
терпит разрыв
,
либо не определена в ), то говорят, что
функция в точке
терпит разрыв
