Одним из основных понятий математики является число. Положительные числа 1,2,3, … , которые получаются при счете, называются натуральными. Числа … -3,-2,-1,0,1,2,3,… называют целыми. Числа, которые могут быть представлены в виде конечного отношения двух целых чисел ( ) называются рациональными. К ним относятся целые и дробные, положительные и отрицательные числа. Числа, которые представляются бесконечными непериодическими дробями называются иррациональными. Примерами иррациональных чисел служат , . В множестве иррациональных чисел выделяют трансцендентные числа. Это числа, которые являются результатом неалгебраических действий. Наиболее известными из них являются число 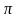и неперово число . Числа рациональные и иррациональные называются действительными. Действительные числа изображаются точками на числовой оси. Каждой точке на числовой оси соответствует одно единственное действительное число и, наоборот, каждому действительному числу соответствует единственная точка числовой оси. Таким образом, между действительными числами и точками числовой прямой установлено взаимно-однозначное соответствие. Это дает возможность равнозначно употреблять термины “число а” и “точка а”.

Переменной называется величина, которая принимает различные численные значения. Величина, численное значение которой не изменяется в данной задаче или эксперименте называется постоянной. Переменные величины обычно обозначают латинскими буквами а постоянные .

Переменная величина считается заданной, если известно множество значений, которые она может принимать. Это множество называется областью изменения переменной.

Интервалом называется множество значений х, заключенных между числами a и b , при этом числа a и b не принадлежат рассматриваемому множеству. Интервал обозначают: ( a, b ); a < x < b.

Отрезком называется множество значений х, заключенных между числами а и b, при этом числа а и b принадлежат рассматриваемому множеству. Отрезок обозначают [a , b] , a≤x≤b. Множество всех действительных чисел является открытым интервалом. ( - ∞,+ ∞ Окрестностью точки х₀ называется произвольный интервал ( а, b ), содержащий точку х₀, все точки этого интервала удовлетворяют неравенству a < x < b.

ε - окрестностью точки а называется интервал с центром в точке а, удовлетворяющий неравенству a –ε < x < a + ε. Обозначают ε(а), здесь – называется радиусом окрестности, -центром окрестности.

Функция. Основные определения и понятия.

Функция является одним из основных понятий математического анализа. Пусть Х и У произвольные множества действительных чисел.

Если каждому числу х  Х по некоторому правилу или закону постав-лено в соответствие единственное вполне определенное действительное число у  У, то говорят, что задана функция с областью определения Х и множеством значений У. Обозначают у = f(х). Переменная величина х называется аргументом функции.

В определении функции существенны два момента: указание области определения и установление закона соответствия.

Областью определения или областью существования функции называется множество значений аргумента при которых функция существует, то есть имеет смысл.

Областью изменения функции называется множество значений у, которые он принимает при допустимых значениях х.

Способы задания функции.

1. Аналитический способ задания функции.

При этом способе задания функции закон соответствия записывается в виде формулы (аналитического выражения), указывающей посредством каких математических преобразований по известному значению аргумента х можно найти соответствующее значение у.

Функция может быть задана одним аналитическим выражением на всей своей области определения или представлять совокупность нескольких аналитических выражений.

Например: у = sin (x² + 1)

2. Табличный способ задания функции

В результате непосредственного наблюдения или экспериментального изучения какого-либо явления или процесса в определенном порядке выписываются значения аргумента х и соответствующие им значения у.

x	X1	X2	x3	…	xn
y	Y1	Y2	y3	…	yn

Эта таблица определяет функцию у от х.

Примером табличного способа задания функции могут служить таблицы тригонометрических функций, таблицы логарифмов, даты и курсы валют, температура и влажность воздуха и т.д.

3. Графический способ задания функции.

Графический способ задания функции состоит в изображении на координатной плоскости точек ( х, у ) посредством технических устройств. Графическим способом задания функции в математическом анализе не пользуются, но к графической иллюстрации аналитически заданных функций прибегают всегда.

График функции

Зададим прямоугольную декартову систему координат хоу и некоторую функцию у = f( х ). Рассмотрим пары соответствующих значений х и f ( х ). Образом этой пары на плоскости служит точка М (х, f(х)). Если переменная х принимает всевозможные значения из области существования функции, получается множество точек плоскости, которое составляет некоторую кривую. Эта кривая называется графиком функции.

1. Функция

Функцией называется отображение множества Х на множество У, при котором каждому элементу х Х соответствует единственный элемент у У.

Это определение можно записать так: 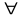х Х, ! у У : х у, или у = f(х) (5.1)

Мы будем рассматривать числовые функции, заданные аналитически, т. е. формулой (5.1.). Множество Х называется областью определения функции и обозначается Д(f). Множество тех значений у У, для которых у=f(х), называется областью значений функции и обозначается Е(f).

Графиком функции у = f( х ) называется множество точек плоскости (хоу) с координатами (х; f( х )).

Функция у = f( х ) называется четной, если 1) область определения ее симметрична относительно начала координат и 2) f(- х ) = f( х ).

Функция у = f( х ) называется нечетной, если 1) область определения ее симметрична относительно начала координат и 2) f( -х ) = - f( х ).

Графики четных функций симметричны относительно оси (оу); графики нечетных функций симметричны относительно начала координат.

Функция у = f( х ) называется периодической, если существует положительное число Т такое, что 1) при всех х Д( f ) числа х + Т и х – Т также принадлежат области определения и 2) f( х + Т ) = f( х ).

Наименьшее положительное число Т, обладающее указанными свойствами, называется основным периодом функции.

Функция называется ограниченной на множестве Х, если существует число С0 такое, что f( х ) С при всех х Х. В противном случае функция называется неограниченной.

Функция у = f( х ) называется возрастающей (убывающей) на некотором множестве Х, если большему значению х Х соответствует большее (меньшее) значение у;

Х, если  и f( )  f( ), то f (возрастающая); если  и f( )f( ), то f  (убывающая).

Функции возрастающие или убывающие называются монотонными.

Рассмотрим функцию у = f( х ), Д( f ) = Х; Е( f ) = У. Каждому элементу у У поставим в соответствие единственное значение х Х, такое, что f( х ) = у. Получим функцию х = ( у ), Д() = У; Е() = Х. Функция  называется обратной для f и обозначается  = и записывается традиционно:у = ( х ) (5.2)

Всякая строго монотонная функция имеет обратную.

Графики взаимно обратных функций симметричны относительно прямой у=х.

Определение. Пусть заданы две функции у = g(х) и z = (у). Область определения функции у содержит область значений функции g. Функция z=(g(х)) называется сложной функцией, составленной из функций g и .