7.Приборы, прим для измерен давления.(атмосфер, избыт, вакуум)

Для измерения давления могут быть применены след приборы: пьезометры, манометры, вакуумметры.

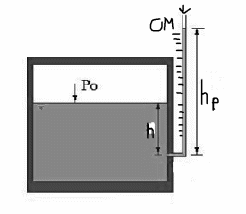В качестве пьезометров обычно исп стеклянные трубки диаметром не менее 0.5 см. нижний конец трубки соед при помощи специал патрубка с той облостью, где должно производ измерение давление. Верхний конец должен быть открытым, сообщающ-ся с атмосферой. Трубка помещ на доске с нанесён на неё измерит шкалой. Если пьезометр подключён к области измерения давленияЮ то жидкость в нём поднимется на пьезометрич высоту hр, измерив кот пошкале, определим избыточ давл в точке резервуара, к кот подключён пьезометр p=Ɣhp. Пьезометры прим для измерен малых давлений (до 0.3-0.4 атм) и в прервую очередь там, где требуется достаточно высок точность измерен. Поэтому пьезом особо широко прим при лаборатор гидравлич исслед.

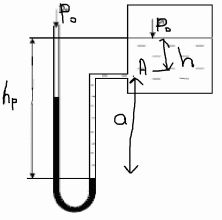Манометры.Наиболее распространены U-обр ртутные манометры, кот при своей простоте обеспеч высок точность измерений. Он сост из стеклян трубки, прикреплён к доске, со шккалой. Один конец трубки соед с областью, в кот необход измерить давл, напр с резервуаром, а другой остается открытым, соед с атмосферой. Трубка заполн ртутью примерно на половину высоты. До подключ манометра к области давл ртуть в обоих коленах будет стоять на одном уровне. После соед манометра с областью давл уровень ртути в колене начнет понижаться, а в другом повышаться до тех пор, пока вся сис-ме не уравновесится. Pабс=Pa+Ɣрт*hp-Ɣ*a.

Ɣ*a – поправка на понижение уровня ртути, это понижение равно высоте а.

Эти манометры позвол измерить давл до 3-4 атм.

Ещё существуют ртутно-чашечный манометр, дифференциальный манометр, механические манометры, пружинный манометр, мембранный манометр.

Вакууметр. Прибор, для измерен величины вакуума. Принцип действия механических и жидкостных вакууметров и описанных выше манометров одинакв, поэтому у них одинаковая конструкция.

8. Дифференциальные уравнения покоящейся идеальной жидкости (Уравнения Л.Эйлера). Вывод уравнений, пример применения уравнений для решения практических задач.

Выберем сист. корд. так, чтобы её грани были параллельны граням параллелепипеда.

На этот параллелепипед жидкости, находящийся в равновесии, действуют:

-сила трения;

-сила со стороны окр. cреды

Р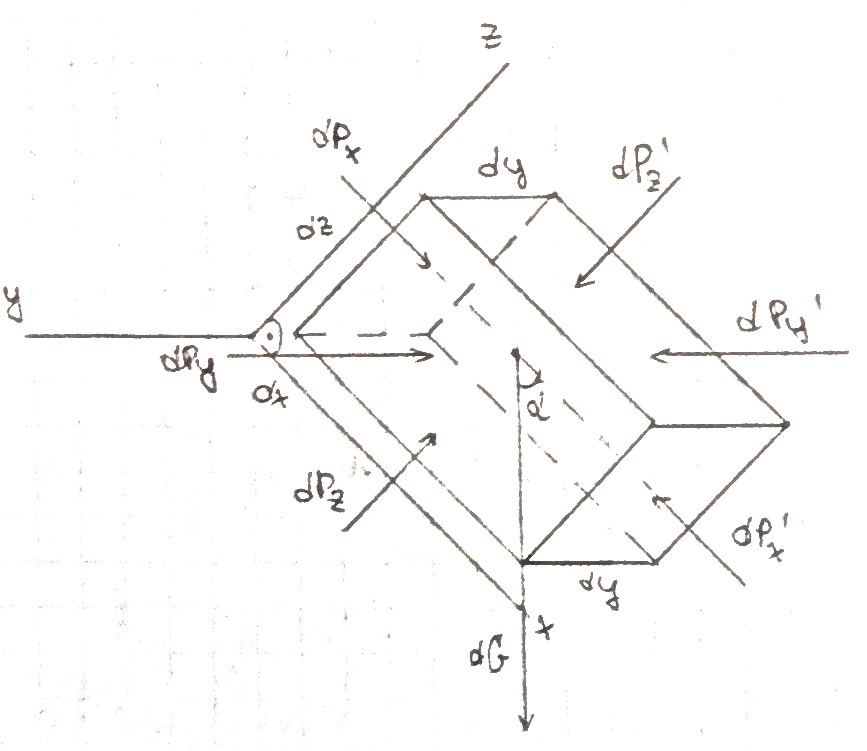 авновесие dV относительно оси X

∑_x=0; dP_x – dP’_x+dGcosα=0

Выясним значения этих сил

dP_x=p_x*dy*dz ;

dP’_x=(p_x+(dP/dx)*dx)*dy*dz ;

dG=ρ*dx*dy*dz*g ;

p_x*dy*dz-p_x*dy*dz -(dP/dx)*dx)*dy*dz+ρ*dx*dy*dz*g=0;

-dp/dx+ ρ*g*cosα=0 , т.к.

x=g*cosα, зн. x-dp/( ρ*dx)=0;

Аналогично для оси z ,y

Получим ДУ Эйлера

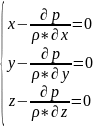
Рассмотрим стандартный пример: найти кратчайший путь между двумя точками плоскости. Ответом, очевидно, является отрезок, соединяющий эти точки. Попробуем получить его с помощью уравнения Эйлера — Лагранжа. Пусть точки, которые надо соединить, имеют координаты и . Тогда длина пути , соединяющего эти точки, может быть записана следующим образом:

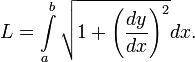
Уравнение Эйлера — Лагранжа для этого функционала принимает вид:

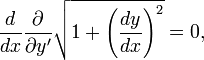откуда получаем, что

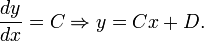Таким образом, получаем прямую линию. Учитывая, что , , т. е. что она проходит через исходные точки, получаем верный ответ: отрезок, соединяющий точки.