31. Уравнение Бернулли для потока реальной жидкости

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии.

где H1-1- напор в первом сечении потока жидкости, H2-2- напор во втором сечении потока, h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

П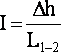 оказателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

П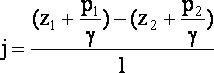 ьезометрическим уклоном называют изменение удельной потенциальной энергии жидкости вдоль потока, приходящееся на единицу его длины.

z– представляет собой нивелирную высоту, то есть расстояние от плоскости сравнения до центра тяжести сечения.

p/2g– пьезометрическая высота, то есть высота на которую поднимается жидкость под действием силы давления.

υ^2/2g – высота скоростного напора, высота на которую поднималась бы жидкость если бы она двигалась вертикально вверх со скоростью υ.

z+p/2g– пьезометрический напор

z+p/ρg+υ^2/2g – гидродинамический напор или линия полной энергии.

Если жидкость невязкая, то гидродинамический напор – горизонтальная линия;

Если жидкость вязкая, то между сечениями будут потери энергии и гидродинамическая линия – наклонная.Если соединить в любой точке все пьезометрические напоры, то получим пьезометрическую линию. Она может иметь положительные и отрицательные значения.

Энерг смысл ур-ия Бернулли-возьмем ур.напора и умнож. на mg:

mgH=mgz+mgp/γ+mυ^2/2

Здесь – mgz-энерг.положения.

mgp/γ-энерг.давления. mgz+mgp/γ-потенц.энерг. mυ^2/2-кинетич.энерг. mgH-полн.энергия.

энерг./mg=удельн.энерг.ед-цы веса.

z- удельн.энерг.положения ед-цы веса

p/γ- удельн.энерг.давления ед-цы веса

υ^2/2g- удельн.кинетич.энерг.ед-цы веса.

32. Ду движущейся идеальной жидкости (ур. Эйлера)

Для вывода уравнения движения жидкости обратимся к записанному ранее уравнении равновесия жидкости (в проекциях на координатные оси), иначе говоря:

Поскольку в идеальной жидкости никаких сосредоточенных сил действовать не может, то последнее уравнение чисто условное. Когда равнодействующая отлична от 0, то жидкость начнёт двигаться с некоторой скоростью, т.е. в соответствии со вторым законом Ньютона, частицы жидкости, составляющие жидкое тело получат ускорение.

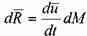
Тогда уравнение движения жидкости в проекциях на координатные оси можно записать в следующем виде:

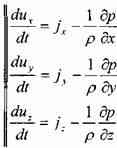
Согласно основному положению о поле скоростей (метод Эйлера) для проекций скоростей движения жидкости можно записать следующее:

или (для установившегося движения жидкости):

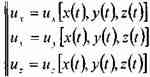
Найдём первые производные от скоростей по времени, т.е. определим ускорения вдоль осей координат:

отметим, что:

Теперь подставив выражения для ускорений в исходную систему дифференциальных уравнений движения жидкости, получим систему уравнений Эйлера в окончательном виде:

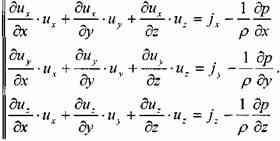
При неустановившемся движении жидкости уравнения Эйлера дополняются первыми слагаемыми.