3. Цепь перемен тока с резистором. Вектор диагр. З-н Ома в компл форме.
Если
к резитив эл-ту приложено синусоид
напряж, то по з-ну Ома для мгнов знач
i=u/R=
Umsin(t+u)/R.
=> ток измен по синусоид з-ну.
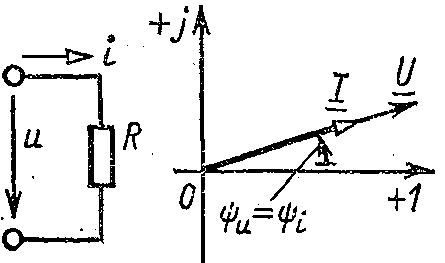
Нач фаза тока i =u, => сдвиг фаз =u-i =0, т.е напряж и ток совп по фазе.
Заменим
мгнов знач комплек выр-ми:
,
разделим U на I:
З-н Ома в компл форме: I=U/R
4.Цепь перемен тока с индуктив эл-том. Вектор диагр.
Синусоид
ток в индуктив эл-те: i=
Imsin(t+i);
,Im=Um,/ωL
– амплитуда тока, I=U,/ωL
– действующее знач, где ωL=XL
- индукт сопротив.
Угол сдвига фаз м/д напряж и током =u-i =90 (график)
Разделим
напряж на ток:
.
З-н ома в компл форме: I=U/jXL.
5. Цепь перемен тока с емк эл-том. Вектор диагр.
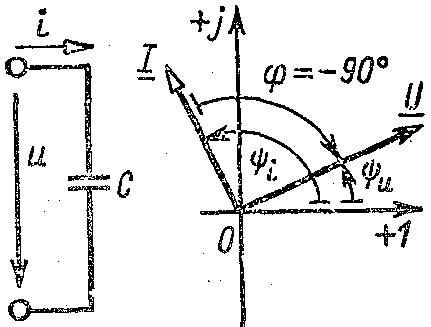ток
на участке цепи с емк эл-том при синусоид
напряж также синусоидален: i=
Imsin(t+i).
Ампл тока Im=UmωС, а его действующ знач I=UωС. Велич, обратная ωС, наз емк сопротивл: ХС=1/ωС
Угол сдвига фаз м/д напр и током: =u-i = -90(график)
З-н ома в компл форме: I=U/Х-jXС
6. Резонанс напряж. Вектор диагр
Рез-с – режим участка цепи, содержащий индук и емкос эл-ты, при к-м разность фаз напр-я и тока участка=0.
Виды: 1. Рез напряж – возможен на уч-ке цепи с послед соед R, L и C, тюе в последоват контуре.
При
рез-се ω=1/LС=ω0,
ω0
– рез-я частота.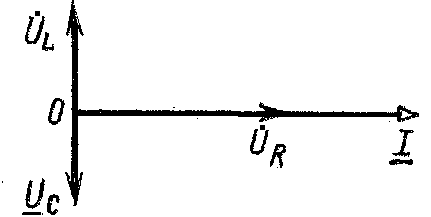
Особ-ти режима рез-са напр:1. =0, то cosφ=1 и суммар сопротивл участка цепи активное.
2.Ток Iрез=U/Zрез=U/R максимален. 3.Напряж на отдел уч-ках контура: UR=RIрез; UL=XLIрез; UC=XCIрез. 4.Актив мощ-ть при резонансе макс, т.к Р=RI2рез, а ток – макс.
2.
Рез токов – возможен в цепи с парал
соед двух ветвей с параметрами R1,
L и R2,
C в параллел контуре.
Особ-ти:
1. =0,
cosφ=1
и общее сопротив контура активное, то
полная проводим-ть контура = актив
провод-ти и практич миним-на. 2.Ток в
незазветвл части цепи практич миним.
3. Реактив составл-щие токов равны и
Iр=Iр1+Iр2=0.
Ток в общей цепи=актив составляющей
тока.
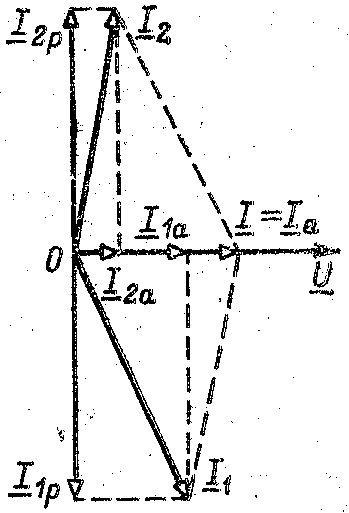
4.Реактив мощ-ти QL=QC, т.к QL=BLU2, QC=BCU2.
7.Цепь перемен тока с послед соед эл-тов. З-ны ома и к-фа в компл форме и для мгнов знач
Если к участку с послед соед эл-тов R, L и C приложено синусоид напряж, то ток в цепи синусоид-е. На кажд из эл-тов будет падать напряж, причем по 2 з-ну К-фа для мгнов знач u=uR+uL+uC. Заменим мгнов знач комплекс выр-ми: U=UR+UL+UC. … U=RI+jXL-JxCI.
З-н ома в комплекс форме: I=U/[R+j(XL-XC)].
8. Мощ-ть цепи синусоид тока (мгнов, актив, реактив, полн). Коэф. мощ-ти.
1.Мгнов мощ-ть – произвед мгнов знач напряж и тока: p=ui. Положит мощ-ть означ, что в участок эл эн поступ энергия, а отриц – уч-к отдает эн.
Мгн мощ-ть уч-ка с последоват-но включ эл-тами: p=uRi+uLi+uCi=pR+pL+pC.
2.Актив – мощ-ть, к-я безвозвратно превращ эл эн в др вид эн: P=UIcosφ (Вт).
3. Реактив – происх обратимые преобраз-я эн: Q=UIsin (вар). Для индуктивэл-та Q =ULI=QL, для емкостного: Q= -UCI= -QC. Если эл-ты соед послед, то Q=QL -QC.
4.Полная – макс возмож мощ-ть при заданных напряж и токе; S=UI.
Связь м/д мощ-тями: S=√P2+Q2
Коэф мощ-ти – отнош актив мощ-ти к полной мощ-ти: cos=P/S. Он пок-ет, какая часть эл эн необратимо преобраз в др виды эн и исп-ся на вып-е полез раб-ты.