Разрешение.

Разрешение (resolution) - количество точек на единицу длины (дюйм, санти­метр). Один из основных параметров изображения. Чем он выше, тем качествен­нее изображение, но больше его файл. За норму принимается 72 пикселя на дюйм (так называемое экранное разрешение), но для получения качественного резуль­тата в полиграфии необходимо значительно больше.

Очень часто в компьютерной литературе разрешение графических файлов обозначают в DPI. Такой подход в корне неверен, DPI - это аббревиату­ра Dots Per Inch (Точек на дюйм) и относится не к файлам, а к мониторам и устройствам ввода-вывода: сканерам, принтерам, цифровым фотоаппа­ратам.

Разрешение изображения и монитора.

Существует одно обстоятельство работы с растровыми изображениями, которое вызывает огромные затруднения у начинающих пользователей. Это несоответ­ствие размеров картинки на экране и ее реальных размеров.

Поясним. Монитор имеет собственное разрешение - количество точек на дюйм. Измеряется оно в DPI (Dots Per Inch). Оно равно 72 или 96 DPI.

Если разрешение изображения соответствует разрешению монитора, то 1 см кар­тинки на экране соответствует 1 см картинки, которая будет выведена на печать.

Но что будет, если разрешение изображения будет выше? Ведь монитор способен отображать максимум один пиксель на точку дисплея. Правильно, размеры картинки на экране визуально будут значительно больше, чем они есть на самом деле.

Интерполяция.

Интерполяция - это математический способ увеличения количества пикселей в растровом изображении, который используется в графических пакетах. Поста­райтесь не путать понятия масштабирование и изменение размеров. Масштабиро­вание (чаще всего оно связано с инструментом ZOOM) это изменение отображения на экране, изменение размеров - внесение изменений в графический файл. По­смотрите на рис. 1.5.

В первом случае, который обозначает масштабирование растровой картинки из четырех пикселей в два раза, количество пикселей никак не изменилось, а размер картинки увеличился за счет увеличения количества точек, отводимых под ото­бражение одного пикселя.

Во втором случае, кроме четырех исходных пикселей, появилось еще двенадцать интерполяционных. Их «додумал» компьютер на основе одной из трех схем.

1. Бикубическая интерполяция. Способ, требующий от компьютера максималь­ной мощности и дающий лучший результат в случае с изображениями, содержа­щими фотографические, со сложными переходами формы и цвета.

2. Билинейная интерполяция. Способ, дающий средний результат при меньших затратах системных ресурсов. Вариант редко используется.

3. По ближнему соседу. Интерполяция, подходящая для одноцветных, простых форм, для которых важно, чтобы они не были размыты. Пример - чертежи.

Векторная графика.

Если в растровой графике базовым элементом изображения является точка, то в векторной графике — линия. Линия описывается матема­тически как единый объект, и потому объем данных для отображения объекта в векторной графике много меньше, чем в растровой графике.

Линия — элементарный объект векторной графики. Как и любой объект, линия обладает свойствами: формой (прямая, кривая), тол­щиной, цветом, начертанием (сплошная, пунктирная). Окончание ли­нии (то есть ее форма в конечном узле) также выступает одним из свойств

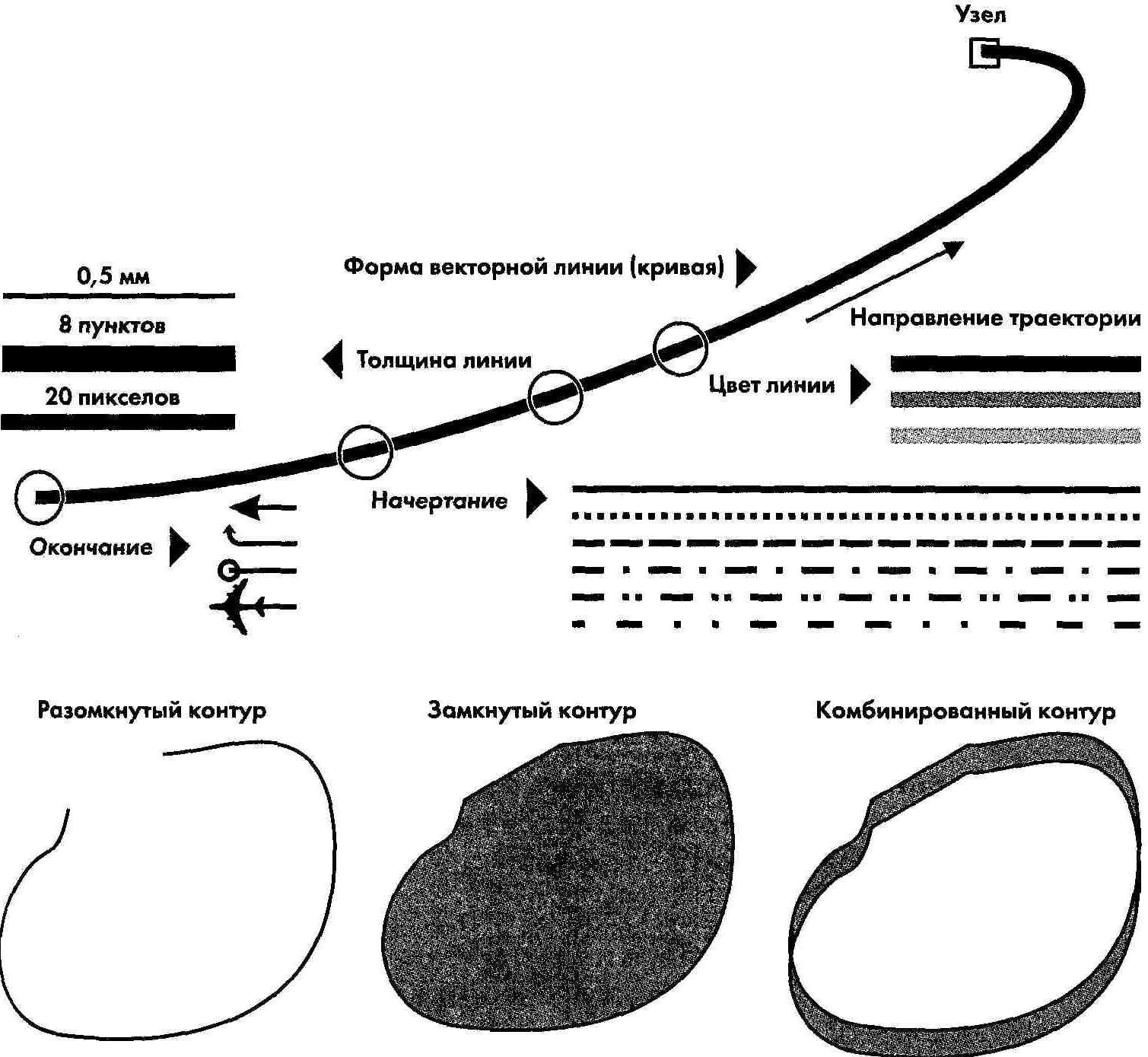
Замкнутые линии приобретают свойство заполнения. Охватываемое ими пространство может быть заполнено другими объектами (например: тексту­ры, карты,штриховки) или выбранным цветом. Заполнение бывает растровым и векторным. В последнем случае иногда используют элементы фрак­тальной графики, являющейся частным случаем векторной. Основ­ные языки программирования при выводе графических примитивов также используют понятия векторной графики.

Простейшая незамкнутая линия ограничена двумя точками, именуе­мыми узлами. Узлы имеют ряд свойств, параметры которых влияют на форму конца линии и характер сопряжения с другими объектами. Все прочие объекты векторной графики, в том числе самые сложные, составляют из линий.

Для построения объектов векторной графики используют инструмен­ты рисования линий и управления заполнением контуров. Простые объекты могут взаимодействовать различными способами, в том чис­ле с применением булевых операций объединения, вычитания и пе­ресечения.

Эффекты, применяемые к объектам векторной графики, воздейству­ют на свойства линии, заполнения и узлов. По сути дела, в програм­мах векторной графики все эти эффекты являются модификаторами. Этот термин хорошо знаком пользователям трехмерных графических при­ложений. Модификатор описывает математическими методами параметры изменения свойств исходного объекта, не затрагивая его основ. Именно на этом базируется возможность многоуровневого «отката», то есть возврата к исходному состоянию объекта.