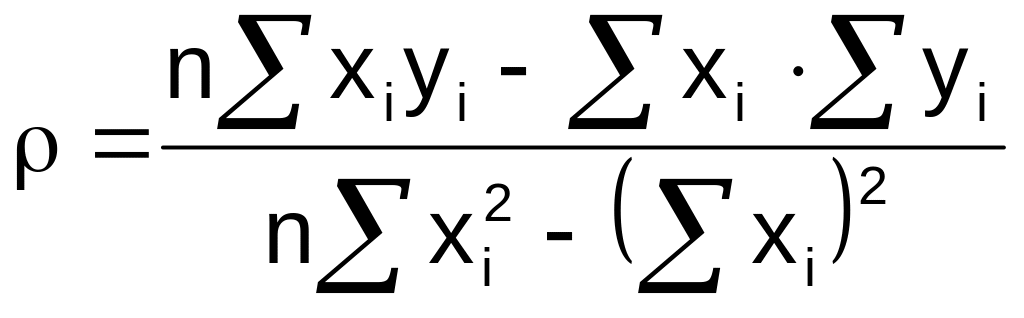- •1. Предмет теории вероятностей. Случайные события, частота. Статистическое и
- •2. Пространство элементарных событий. Алгебра событий. Классическое определение вероятности.
- •3. Теоремы сложения и умножения вероятностей. Условная вероятность. Зависимые и
- •4. Формула полной вероятности. Формула Байеса.
- •5. Повторение испытаний. Формула Бернулли.
- •6. Локальная и интегральная теоремы Лапласа. Функция Лапласа. Формула Пуассона.
- •7. Дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины. Биномиальное распределение, распределение Пуассона.
- •8. Интегральная функция распределения (функция распределения), свойства, график.
- •9. Дифференциальная функция распределения (плотность распределения), свойства, график.
- •10. Числовые характеристики случайных величин. Математическое ожидание дискретных и непрерывных случайных величин.
- •11. Дисперсия и среднеквадратическое отклонение дискретных и непрерывных случайных величин.
- •12. Начальные и центральные моменты распределения, асимметрия, эксцесс, мода, медиана.
- •13. Равномерное и показательное распределения, функция надежности.
- •14. Нормальное распределение.
- •15. Понятие о предельных теоремах. Закон больших чисел, центральная предельная теорема.
- •16. Предмет математической статистики и ее основные задачи. Основные понятия (выборка, объём выборки, варианты, статистический ряд, интервальный ряд).
- •17. Эмпирическая функция распределения, полигон, гистограмма.
- •18. Определение неизвестных параметров распределения (выборочная средняя, выборочная и исправленная выборочная дисперсии).
- •20. Понятие корреляционной зависимости. Коэффициент корреляции, положительная и отрицательная корреляции. Функции и линии регрессии.
20. Понятие корреляционной зависимости. Коэффициент корреляции, положительная и отрицательная корреляции. Функции и линии регрессии.
Определение. 2 случ. величины X и Y находятся в корреляционной зависимости если каждому значению одной из них соответствует определенное распределение вероятности другой.
Коэффициент корреляции безразмерная величина
![]()
![]()
св-ва коэффициента корреляции:
1) если X и Y независимые сл. величины, то R(x,y)=0. Обратное не всегда верно.
2) Для всех X, Y |R(x,y)|<=1. Если |R(x,y)|=1 то X и Y связаны линейной зависимостью.
R(x,y) хар-зует только лин. корреляционную зависимость, кот. состоит в том, что с увеличением одной из случайных величин, вторая имеет тенденцию увеличиваться, причем R – определяет степень близости корреляционной зависимости к линейной. Чем ближе R к единице, тем зависимость между X и Y ближе к линейной, чем ближе R к нулю, то либо X, Y независимые, либо зависимость корреляционная, но не линейная.
Если R>0 то говорят о положительной корреляции, если R<0 то – об отрицательной.
Пусть X и Y непр. случ. величины, находящиеся вв корреляционной зависимости.
Определение. Плотность распр. случ. величины Y равная fx(y), при условии X=x, наз. условной плотностью распределения Y.
Вычислим мат. ожидание
![]()
Эта функция наз. функцией регрессии Y на X. Аналогично
![]()
Функции φ(x) и g(x) линейные
Доказано, что ур-е линии регрессии имеет вид:
ур-е линейного распределения (Y на X):
![]()
ур-е линейного распределения (X на Y):
![]()
![]()
![]()
![]()
Ур-е линии регрессии имеет вид:
y=ρx+b, где