1.Схема Бернулли

30. В чем состоит схема Бернулли? Запишите формулу для вероятности успехов в серии испытаний по схеме Бернулли и приведите пример ее применения.

Схема Бернулли: производится n независимых испытаний, в каждом из которых с одной и той же вероятностью p наступает некоторое событие А (называемое обычно «успехом») и, следовательно, с вероятностью q=1-p наступает событие , противоположное А.

Пусть k – любое из чисел 0,1,2,…,n. Обозначим вероятность того, что в n испытаниях Бернулли успехов наступит k раз. Справедлива формула Бернулли:

.

Пример: Монета бросается 10 раз. Какова вероятность того, что герб выпадает при этом ровно 3 раза?

Решение: В данном случае успехом считается выпадение герба, вероятность p этого события в каждом опыте равна ½ , так что q=1-p=1|2. Отсюда

.

33. Пусть – вероятность успехов в серии независимых испытаний с вероятностью успеха в каждом испытании. При каком вероятность достигает максимума? Совпадает ли это число с математическим ожиданием количества успехов? Чему равна сумма ?

Рассмотрим два соседних числа и . Между ними имеет место одно из соотношений: (меньше, равно или больше) или, что эквивалентно, . Подставляя вместо числителя и знаменателя их выражения по формулам , или учитывая, что , получим соотношения или . Собирая все слагаемые с множителем k и учитывая , что p+q=1 , получим эквивалентные соотношения . Обозначим число np+p через . Тогда перепишется : .

Таким образом, для всех значений k меньших чем справедливо неравенство , для ( это возможно только в том случае, когда - целое число) имеет место равенство , наконец, при выполняется неравенство . Тем самым при значениях функция возрастает, а при значениях убывает. Следовательно, если число не является целым, то функция имеет единственный максимум; он достигается при ближайшем к слева целом значении k , т.е. при таком целом , которое заключено между -1 и : np-q< <np+p, =[np+p].

Если же - целое число, то два равных между собой максимума достигается при и .

Если число не является целым, то наиболее вероятное число успехов равно ближайшему к слева целому числу. В случае когда есть целое число, наиболее вероятное число успехов имеет два значения: -1 и . Сумму не знаю как посчитать.

34. Может ли наиболее вероятное число успехов в схеме Бернулли отличаться от математического ожидания числа успехов на 2? Ответ обоснуйте.

По схеме Бернулли наиболее вероятное число успехов: k=np+p.

Мат. ожидания: так как схему Бернулли можно представить как биноминальное распределение E(x)=np

np+p-np=p Следовательно, в схеме Бернулли наиболее вероятное число успехов может отличаться от мат. ожидания на число р - вероятность успеха и известно, что p+q=1, p=1-q p<1. А значит отличаться на 2 не может.

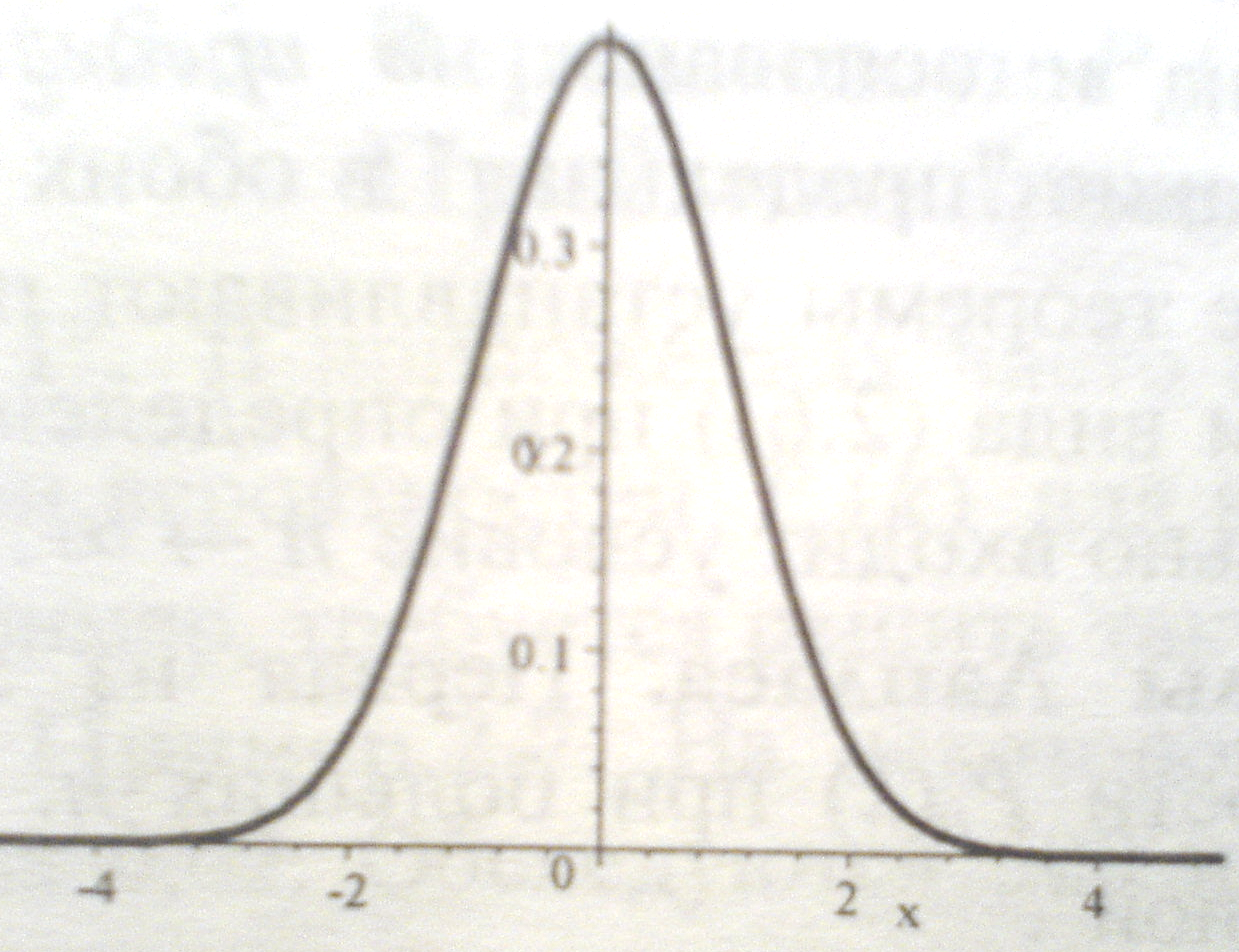
35. Запишите локальную приближенную формулу Лапласа, приведите основные свойства функции Гаусса и укажите ее график. При каких условиях данная формула дает хорошее приближение? Какие условия применимости отличают эту формулу от приближенной формулы Пуассона?

Если число опытов достаточно велико но не бесконечно, а вероятность появления события А в каждом опыте не стремится к 0, применяют локальную и интегральную теоремы Лапласа

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р причем 1>р>0, то это событие наступает ровно m раз приблизительно равна

36. Запишите интегральную приближенную формулу Лапласа и приведите основные свойства функции Лапласа . При каких условиях данная формула дает хорошее приближение?

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р, причем 1>р>0, то событие А наступит не менее m₁ раз и не более m₂ раза приблизительно равно

Хорошее приближ. При больших n

37. Укажите выражение для функции Лапласа . Докажите нечетность функции и нарисуйте график . Чему равно ?

Функция: Ф(x) =

Д оказ-во Ф(-x) = -Ф(x): запишем выражение Ф(-x) = и выполним замену z = -t, dz = -dt, при этом нижний предел интегрирования не изменится, а верхний станет равным x. Таким образом, Ф(-x) = = -Ф(x), ч.т.д.

График: симметричен относительно начала координат, проходит через (0;0). Горизонтальные асимптоты: -0,5 и 0,5.

Ф(12) = 0,5.

39. Сформулируйте и докажите предельную теорему Пуассона.

При n, p0 b, а величина  = np остаётся постоянной .

Док-во: имеем: , и так как p=/n, то . Выражение - это произведение k множителей, стремящихся к 1; поэтому и всё произведение стремится к 1. Выражение стремится к 1. Что касается выражения , то его можно записать в виде . Замечая, что выражение в квадратных скобках имеет пределом число , получим окончательно: , где 1. Отсюда тотчас же следует формула, указанная в теореме.