4. Какие события называются достоверными и невозможными и каковы их ве-роятности? Пусть a, b и c – случайные события. Перечислите все случаи наступления события .

Событие А, которое произойдет при любом испытании, называется достоверным

(А = ). Например, в опыте с подбрасыванием игральной кости событие А, задаваемое условием “число выпавших очков положительное”, будет достоверным. Вероятность достоверного события равна 1.

Событие А, которое не может произойти при испытании, называется невозможным (А=пуст.множ.). Например, событие А, задаваемое условием “при подбрасывании игральной кости выпало 7 очков”, является невозможным. Вероятность невозможного события равна 0.

Таблица, характеризующая событие А +С

А	В	С	А +С
1	1	1	1
1	1	0	0
1	0	1	1
1	0	0	1
0	1	1	1
0	1	0	0
0	0	1	1
0	0	0	0

5. В каком случае событие в называют следствием события а? Какие события называются равными? Объясните, почему .

Событие А влечет за собой событие В или событие В является следствием события А (А В), если каждый исход, благоприятный для А, является благоприятным и для В. События А и В равны (А=В) в случае, когда они являются следствиями друг друга.

I) А АВ+А

Если А наступило(А=1), то: 1) если В при этом наступило, то наступило АВ АВ+А наступило; 2) если В не наступило, то =1 А =1 АВ+А наступило.

II) АВ+А А

Если АВ+А наступило, то либо АВ наступило (т.е А наступило АВ+А А) либо наступило А (А наступило АВ+А А).

Событие А наступает, т.к. любое событие А попадает в В или . А=А( )=А* =А.

6. Пусть а и в – случайные события. Упростите выражение . Найдите событие, противоположное событию .

(А+В)(А+ ) = АА+А +АВ+В =А+А(В+ )

7. Докажите, что . Что означает событие ?

= * *…..* . Наступление события А +….А означает, что наступает по меньшей мере одно из событий А ,….,А . Наступление противоположного события означает, что не наступает ни одно из событий А ,….,А или, по-другому, что наступают одновременно все события ,…., , но это в точности означает наступление события * *…..* . Ч.т.д.

А А + А А + А А : означает наступление ровно двух событий из трех.

8. Докажите, что = + +…..+ . Что означает событие А А + А А + А А ?

= + +…..+ . Наступление события А *….*А означает, что наступают каждое из событий А ,….,А . Наступление противоположного события означает, что не наступает хотя бы одно из событий А ,….,А или, по-другому, что наступают события + +…..+ . Ч.т.д.

А А + А А + А А : означает наступление не меньше двух событий.

9. Сформулируйте статистическое определение вероятности. Почему вероятность удовлетворяет условию 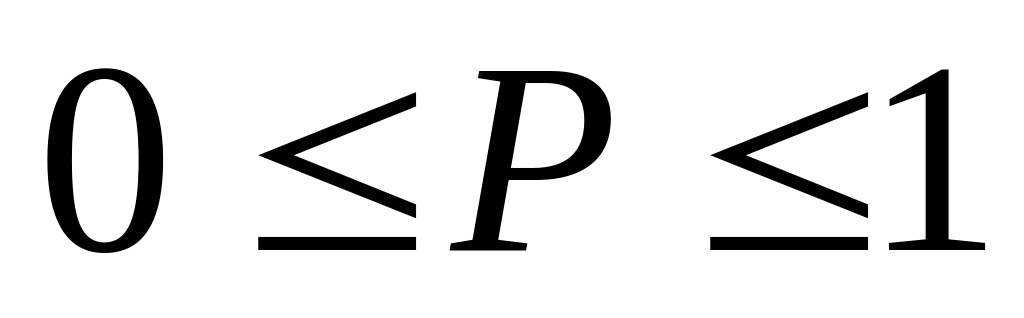? Возможны случаи Р=0 и Р=1? Ответ обоснуйте.

Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит, 0<m/n<1, следовательно, 0<P(A)<1. Вероятность любого события удовлетворяет двойному неравенству 0≤Р(А)≤1.

В качестве статистической вероятности события понимают относительную частоту или число, близкое к ней. Свойства вероятностей вытекают из классического определения и сохраняются для статистического.

А – случ.событие

N – кол-во опытов, N -благ.

Р(А)= , где N N, N 0.

А- выпала игральная кость, числа которой > 7, P(A)=0

В- выпала игральная кость, числа которой < 7, P(A)=1

10. Какие соб.A1,A2,…An называются попарно несовместными? Сформулируйте правило сложения вер-тей для попарно несовместных соб. A1, A2, …An. Приведите пример попарно несовместных событий A,B, и C, таких что P(A+B+C)<1?

A1,A2,…An – попарно несовместны, если они никогда не выполняются одновременно. Исходя из следствия, можно сказать, что вер-ть появления одного из нескольких попарно несовместных соб., безразлично какого, равно сумме вер-тей этих соб. P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).Док-во: Рассмотрим 3 соб.A,B,C. Т.к. рассматриваемые события попарно несовместны, то появление одного из трех событий, A,B,C, равносильно наступлению одного из двух соб,A+B и C, поэтому в силу указанной теоремы

P(A+B+C)=P =P(A+B)+P(C) =P(A)+P(B)+P(C).

Пример: Существуют 5 карточек с написанными цифрами: 1,2,3,4,5. 

. Соб.А – вытащили карточку с числами, делящимися на 2, В – делящ. на 3, С – делящ. на 5. События А,В,С попарно независимы. АВ= , АС= , ВС= .  P(A+B+C)=P(A)+P(B)+P(C).

, , P(A+B+C)=0,4+0,2+0,2=0,8<1

11. Объясните, почему Р(А+В)≤Р(А)+Р(В) для событий A и B. Чему равна сумма P(A)+P( ) вероятностей противоположных событий? Ответ обоснуйте.

А и В – как сов., так и несов. события.

Р(А+В)=Р(А)+Р(В) - Р(АВ)

Когда мы считаем P(А+В), то при сложении Р(А) и Р(В) мы дважды учитываем пересечение, то есть его надо вычесть:

Р(А)+Р(В)=Р(АВ)+Р(АВ)+Р(А+В)- Р(АВ)Р(А)+Р(В)=Р(АВ)+Р(А+В)

Р(А+В)=Р(А)+Р(В)-Р(АВ)

Р(А+В)≤Р(А)+Р(В) Исходя из следствий (теорема сложения вероятностей) можно сказать, что сумма вероятностей противоположных событий равна единице. P(A)+P( )=1. Т.к. события A и несовместны, поэтому можно применить формулу P(A+B)=P(A)+P(B). При этом следует использовать то, что событие A+ - достоверное, поэтому его вер-ть =1.Также используют такую формулу, выражающую вер-ть события A через вер-ть противоположного события . P(A)=1-P( )

12. Верно ли, что если событие A является следствием события B,то P(A) ≤ P(B)? Ответ обоснуйте.

Да, верно, т.к. согласно следствию: если соб B явл. следствием соб. A, то P(A) ≤ P(B). Т.к. A B, то B=A+(B/A)- сумма несовместных событий. Применяя правило сложения вер-тей, имеем P(B)=P(A)+P(B/A), откуда следует неравенство P(A) ≤ P(B)