Методы и алгоритмы структурного синтеза (структурной оптимизации)
Этих подходов много, выделяют 7 основных.
1) Методы полного перебора. При реализации полного перебора необходимо упорядочить множество исследуемых вариантов с тем, чтобы исключить возможность пропуска вариантов или анализа одних и тех же вариантов, более чем по одному разу.
2) Метод ветвей и границ. Под этим названием фигурирует целая группа комбинаторных методов частичного перебора. Эти методы идеи заключаются в том, что на каждом шаге поиска вместо оценки отдельного варианта, осуществляется оценка группы вариантов, если результат такой оценки отрицательный, то из дальнейшего рассмотрения исключается не один вариант, как в методе полного перебора, а группа вариантов, что существенно уменьшает число шагов поиска. Алгоритмы метода ветвей и границ включают следующие процедуры:
- разбиение конечного множества вариантов на несколько подмножеств
- формулировка для каждого подмножества задачи, решения которой можно было бы рассматривать как оценку перспективности данного подмножества. Подмножество считается перспективным, если среди его элементов может находиться вариант наилучший в смысле принятого критерия оптимальности.
- решение сформулированной задачи для каждого из подмножеств
- выделение для дальнейшего рассмотрения перспективных подмножеств.
Названные процедуры повторяются по отношению к выделенным подмножествам. Поиск прекращается, когда в единственном выделенном подмножестве оказывается единственный вариант. Для применения методов ветвей и границ нужно иметь, во-первых, правила разбиения множества вариантов на подмножество родственных вариантов и, во-вторых, алгоритм оценки перспективности подмножеств.
Сам метод ветвей и границ не устанавливает таких правил для общего случая. Эти правила оказываются специфичными для каждого класса задач.
3) Метод «и-или» дерева (графа)
4) Методы последовательного синтеза в этих алгоритмах выбирается некоторый начальный элемент, к которому поочередно по определенным правилам добавляются новые элементы вплоть до образования законченной структуры. Примерами задач, решаемых в системах автоматизированного проектирования в автоматическом режиме с помощью последовательного синтеза, служат задачи компоновки, размещения и трассировки.
Последовательный алгоритм компоновки для задач конструирования радиоэлектронных устройств. Задача заключается в размещении, распределении элементов устройства по блокам. В качестве элементов выступают корпуса микросхем, а в качестве блоков ТЭЗ-ы, связанные между собой с помощью разъемных соединений, при такой конструкции очевидно, что количество соединений между блоками желательно иметь как можно меньше, при этом упрощается конструкция и возрастает помехоустойчивость, т.к. общая длина электрических соединений между блоками уменьшается, поэтому алгоритм компоновки. Алгоритм компоновки целесообразно создавать как алгоритм минимизации количества межблочных связей.
Пусть в очередной j-ый блок уже помещено некоторое количество элементов, тогда производится просмотр всех не скомпонованных элементов и среди них выбирается для включения в J-ый , тот элемент, который имеет наибольшее число связей с элементами, уже находящимися в этом блоке, если таких элементов несколько, то включается тот из них, который имеет наименьшее число связей с еще нераспределенными элементами. Компоновка j-го блока начинается с помещением в него одного произвольного элемента, и заканчивается, когда блок будет заполнен полностью, либо, когда будет превышено допустимое число внешних связей j-го блока.
Последовательные алгоритмы размещения. Они используются для получения некоторого исходного варианта, который в дальнейшем предстоит улучшить с помощью итерационных алгоритмов. Перед началом исполнения последовательного алгоритма размещения, обычно бывает задано положение некоторых элементов, например, при размещении элементов радиоэлектронного устройства на плате, может быть задано расположение контактных площадок для внешних выводов, тогда задача размещения заключается в определении очередности установки новых элементов и в определении местоположения очередного размещаемого элемента. Существует много разновидностей последовательных алгоритмов размещения. Рассмотрим в кратком изложения один их них:
Пусть А – множество размещаемых элементов, Б – множество уже размещенных элементов, В – множество еще не размещенных элементов. Пусть критерий размещения вытекает из требования минимизации общей длины коммуникации. В соответствии объекту можно подставить граф, в котором вершины отображают элементы объекта, а ребра – связи между элементами. Тогда в качестве исходных данных можно использовать матрицу смежностей.
Очередным размещаемым элементом должен быть элемент, имеющий наибольшее число связей с уже размещенными. Для многих задач размещения в качестве целевой функции целесообразно иметь величину суммарной длины связей с уже размещенными элементами.
Алгоритм трассировки печатных плат. Волновой алгоритм. Пусть трассируются электрические соединения на печатной плате. Все монтажное поле печатной платы делим на квадраты с размерами определяемыми шириной проводников, с учетом зазоров между ними. Из исходной точки .а имитируется распространение волны, это делается путем нумерации цифры 1 всех квадратов, прилегающих к исходному. Цифрой 2нумеруются квадраты, прилегающие к квадратам с 1, и т.д. Крестами отмечены занятые квадраты. .b – конечная точка трассы. Фронт фолны отображается совокупностью квадратов с одинаковыми номерами распространяется из а пока не дойдем до b, после этого прокладывается трасса, начиная из конечной точки b по квадратам с номерами последовательно уменьшающимися, на рисунке построенная трасса показана штрихами.
7 |
8 |
|
8 |
7 |
8 |
|
|
6 |
7 |
8 |
Х |
6 |
7 |
8 |
|
5 |
Х |
Х |
Х |
5_ |
_6 |
_7 |
.b |
4 |
3 |
_2 |
_3 |
_|4 |
Х |
8 |
|
3 |
2 |
| 1 |
Х |
Х |
Х |
7 |
8 |
2 |
1 |
| .a |
1 |
Х |
5 |
6 |
7 |
3 |
2 |
1 |
2 |
3 |
4 |
5 |
6 |
4 |
3 |
2 |
3 |
Х |
Х |
Х |
Х |
Волновой алгоритм не гарантирует проведение соединений без пересечений и без переходов на другие слои, даже в случаях, когда такое проведение возможно.
На втором рисунке приведен пример результатов трассировки, здесь линии из точек – трассы проведенные по волновому алгоритму, а трассу D-D’ без пересечений провести не удается. Если же трассу C-C’ провести по более длинному пути (линия из черточек), то трассировку можно выполнить полностью, поэтому часто в автоматическом режиме задают некторый исходный вариант трассировки, и дальше этот вариант дорабатывается, либо инженером вручную, либо в диалоге с ЭВМ.
|
|
|
|
|
|
|
|
|
|
|
|- |
-------- |
-------- |
-------- |
-| |
|
. |
……... |
. | |
|
|. |
. |
| |
|
. |
‘D’ |
‘C’ |
‘B’ |
‘A’ |
. |
| |
|
. |
.. |
.. |
.. |
..| |
. |
| |
|
. |
.. |
. |
. |
. |
. |
| |
|
. |
|.. |
|. |
|- |
-------- |
-------- |
-| |
|
. |
A |
B |
C |
D |
|
|
|
. |
........... |
........... |
.| |
|
|
|
|
|
|
|
|
|
|
|
5)Итерационные алгоритмы сокращенного перебора. Они являются алгоритмами улучшения первоначально заданной структуры, по своей сути это алгоритмы перебора, в которых каждый очередной вариант структуры образуется по определенному правилу и перебор заканчивается, когда следование этому правилу не позволяет добиться дальнейшего улучшения. Количество проб здесь существенно меньше, чем при полном переборе, но нет гарантии получения наилучшего, т.е. оптимального решения. В качестве примера итерационного алгоритма рассмотрим алгоритм парных перестановок для решения задачи размещения элементов.
В заданной структуре выбирается очередной элемент ai из множества А. Осуществляется перестановка элемента ai c aj, при этом i<>j. Получившийся новый вариант представляет собой новую пробу. Для этого варианта подсчитывается значение целевой функции. Следующий вариант структуры будет отличаться от исходного тем, что элемент ai меняется местами с элементом ak, где k<>i и k<>j, такие парные перестановки элемента ai осуществляются со всеми остальными элементами множества А. Получаем n-1 проб. Из вариантов выбирается один, для которого значение целевой функции окажется экстремальным, данный вариант рассматривается как новое исходное размещение, и в этом варианте структуры выбиарется новый элемент a[i+1] для парных перестановок со всеми остальными элементами.
Перебор всех элементов для осуществления парных перестановок требует выполнения n*(n-1) проб. Очередность выбора элемента множества А для парных перестановок с остальными элементами может быть произвольной, но лучше начинать перестановки с элементов, имеющих наибольшее число связей с остальными. Если на двух соседних итерациях не достигнуто улучшение целевой функции, то задача размещения считается решенной. Обычно требуется сравнительно малое число итераций и поэтому общее число проб существенно меньше, чем n!.
6) Методы дискретного математического программирования. Их принято делить на методы отсечения, комбинаторные методы и приближенные.
Методы отсечения. В методах отсечения решение исходной задачи происходит с помощью многократного решения вспомогательной задачи, более простой, чем исходная. На каждом этапе. На каждом этапе решения полученные результаты позволяют уточнит задачу так, что в итоге последовательность решений вспомогательной задачи сходится к решению исходной. Методы отсечения наиболее развиты в применении к задачам целочисленного линейного программирования, одним из таких методов является метод Гомори. Вспомогательной задачей здесь выбрана задача линейного программирования со снятыми ограничениями целых чисел. На каждом этапе решения вспомогательной задачи позволяет ввести новое ограничение, которое отсекает часть допустимой области такую, в которой не может находиться искомое целочисленное решение. Метод Гомори приводит к получению экстремума за конечное число решений вспомогательной задачи.
Комбинаторные методы. Среди них наиболее известные: метод ветвей и границ и метод последовательного анализа вариантов. В дискретном программировании эти методы удается использовать тогда, когда имеются правила корректной оценки результатов решения промежуточных задач. Наличие таких правил обеспечивает нахождение экстремума, поэтому эти методы дискретной оптимизации называют точными. К сожалению, точные методы оказываются неэффективными при решении большинства задач высокой размерности. Так как для них характерен полиномиальный или даже экспоненциальный рост трудоемкости вычислений с увеличением числа параметров, поэтому в практике решений задач дискретной оптимизации широкое распространение получили методы третьей группы (приближенные). Их применение не гарантирует получение экстремума, однако, если при применении вероятность получения экстремума довольно высока, а трудоемкость его поиска сравнительно мала, то метод оказывается удобным для применения. В качестве примера приближенного метода рассмотрим метод локальной оптимизации.
В этом методе сокращение трудоемкости достигается за счет замены полного перебора во всех точках Х ОДЗ полным перебором в сравнительно малой окрестности текущей точки, изображающей точки Xi. Пусть в окрестности рассматриваемой точки находится r точек и Xk, где k=1..n. Полный перебор точек Xk означает, что для всех этих точек вычисляются значения целевой функции. Пусть f(Xq) является минимальным для всех точек из числа k, если f(Xi) больше f(Xq), то переходим к очередному шагу поиска, приняв в качестве текущей отображающей точки точку Xq, а если нет – заканчиваем, поэтому поиск следует, либо прекратить, приняв эту точку за оптимальную, либо продолжить, расширив исследуемую окрестность исследованной точки Xi.
7) Геометрическое проектирование. Под геометрическим проектированием понимается решение задач, направленных на определение геометрических свойств проектируемых объектов и на отображение этих свойств в графической форме средствами машинной графики. Некоторые задачи:
- определение формы поверхности корпусов судна, фюзеляжей самолетов, корпусов автомобиля.
- расчет траектории движения режущего инструмента (в станках)
- формирование графического образа проектируемого изделия с помощью процедур определения поверхности пересечения двух тел, формирования плоских сечений, определение третьей проекции объекта по двум заданным, совмещение изображений нескольких слоев топологии интегральной микросхемы и т.д.
- двумерные и трехмерные преобразования графических образов, включающих операции сдвига изображения, поворота, отсечения части рисунка.
Мат аппаратом для решения большинства перечисленных задач является вычислительная геометрия. Напомним некоторые методы решения задач геометрического проектирования. В задачах проектирования поверхностей сложной формы, поверхность представляется в виде сетки, значение координат в узлах которой, являются заданными, при этом ищется подходящая аппроксимирующая поверхность с получением его математического описания. Недостатком такого подхода является то, что при малой степени полинома возможны заметные отклонения узлов сетки от поверхности, а при высокой степени полинома появляется волнистый характер поверхности, поэтом на практике часто более удачной является аппроксимация сплайнами. Часто используются кубические сплайны.
При двумерных преобразованиях графических объектов производится пересчет координат все точек объекта по несложным формулам:
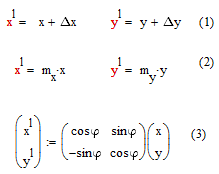
1 – перемещение
2 – масштабирование
3 – поворот
4 – отсечение
Операция отсечения заключается в отбрасывании той части изображения, которая находится вне заданного прямоугольника
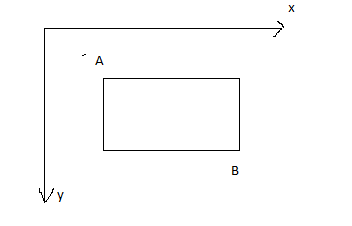
Пусть прямоугольник задан вершинами А=(xa,ya) B=(xb,yb) такими, что xa<xb и уa<yb, тогда точка с координатами (x,y) отбрасывается, если выполняется хотя бы одно из четырех следующих условий: x<xa; x>xb; y<ya; y>yb
Такими же несложными проверками можно установить расположен ли заданный отрезок прямой полностью в прямоугольнике, либо полностью вне него, либо частично в прямоугольнике.