3. Графоаналитический способ

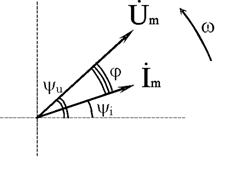Рис. 2.2

Графически синусоидальные величины изображаются в виде вращающегося вектора (рис. 2.2). Предполагается вращение против часовой стрелки с частотой вращения ω. Величина вектора в заданном масштабе представляет амплитудное значение. Проекция на вертикальную ось есть мгновенное значение величины.

Совокупность векторов, изображающих синусоидальные величины (ток, напряжение, ЭДС) одной и той же частоты называют векторной диаграммой.

Использование векторных диаграмм позволяет существенно упросить анализ цепей переменного тока, сделать его простым и наглядным.

В основе графоаналитического способа анализа цепей переменного тока лежит построение векторных диаграмм.

4. Аналитический метод с использованием комплексных чисел

Рис. 2.5

Синусоидальный ток i(t) = I_m sin(ωt + ψ) можно представить комплексным числом Í_m на комплексной плоскости (рис. 2.5)

Í_m = I_me^jψ,

где амплитуда тока I_m – модуль, а угол ψ, являющийся начальной фазой, – аргумент комплексного тока.

7)Понятие о комплексном и полном сопротивлении цепей синусоидального тока.

Отношение комплексного напряжения к комплексному току называется комплексным сопротивлением:

Z=U/I=Um/Im=zej=z, 

где z=U/I=Um/Im — отношение действующего или амплитудного напряжения соответственно к действующему или амплитудному току называется полным сопротивлением. Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т. е. =u—i. Комплексное сопротивление можно представить в виде

Z=zej=zcos+jzsin=r+jx,  где r=zcos — действительная часть комплексного сопротивления, называется активным сопротивлением; x=zsin — значение мнимой части комплексного сопротивления, называется реактивным сопротивлением

Полное сопротивление определяют на основании закона Ома по показаниям вольтметра и амперметра:

Z = U / I

8)Идеальный резистивный элемент в цепи синусоидального тока

Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение  то ток i через него будет равен

.

(1)

Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и  i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.

Из (1) вытекает:

;

.   

9 )Идеальный индуктивный элемент в цепи синусоидального тока

Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток определяется выражением . Тогда для напряжения на зажимах катушки индуктивности можно записать

.

(5)

Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на /2.

Введенный параметр называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты