68. Сүзгілер, тжс. Олардың қасиеттері , .

Электрлік сүзгі

Белгілі жиіліктердің алқабын шамалы өшуімен өткізетін, ал бұл жиілік алқаптың сыртындағы дабылдарды – күшті өшуімен өткізетін пассивтік төртұштық. Өшу шамалы алқап өткізу алқап деп аталады, басқа жиіліктер саласы – өшу алқап деп аталады.

16.1 К е с т е  Сүзгілерді топтастыру

Сүзгілер атауы	Жиілікті өткізу диапазоны
Төменгі жиіліктердің сүзгілер (ТЖС)
Жоғары жиіліктердің сүзгілер (ЖЖС)
Жолақ алқапты өткізгіш сүзгілер (ЖӨС)
Бөгегіш сүзгілер (БС) немесе шекаралық сүзгілер (ШС)	және мұндағы

жиілігі жиілік қимасы немесе шекаралық жиілігі деп аталады.

Сүзгілер радиотехникада және байланыс техникасында қолданылады, мұнда күштік электроникада мен электротехникадағы сияқты жоғары жиілікті тоқтар болады.

Қолданылуы LC – пассивтік сүзгілер және RC – сүзгілер; активтік RC – сүзгілер (АRC-сүзгілер); сандық сүзгі.

ТЖС – нің сипаттамалық кедергісі

15 Дәрісте Т және П симметриялық сұлба үшін сипаттамалық кедергі алынды

, .

Осыдан ТЖС үшін сипаттамалық кедергі аламыз

. (17.5)

. (17.6)

(17.5) және (17.6) теңдігінен шығатыны, сипаттамалық кедергі жиілікке тәуелді, кезінде: , 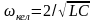кезінде: , .

Өткізу жолағында сипаттамалық кедергі активті болады. Жүктеме-нің сүзгімен келісуі кезінде ( ) сүзгінің кіріс кедергісі 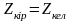болады, осыдан шығатыны, сүзгінің кірісінде тоқ және кернеу фазасы бойын-ша сәйкес келеді және өткізу жолағында сүзгі резонанс тәртібінде жұмыс жасайды.

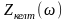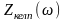, тәуелділігі 17.3 суретінде көрсетілген. Сондай – ақ сипаттамалық кедергі жиілікке тәуелді болады, сондықтан барлық жиілік диапазонындарында сүзгі жүктемемен келіспейді.

69. Синусоидалды емес тоқ тізбегінің қуаттары.

Периодты синусоидальды емес тоқтың тізбектеріндегі қуаты

Кернеу мен тоқтың лездік мәндерін тригонометриялық қатар түрінде жазайық

.

Онда, актив қуат үшін былай жазуға болады

(13.4) Интегралдағаннан кейін аламыз

(13.5)

Осыдан, синусоидальды емес тоқтың актив қуаты актив қуаттардың бөлек гармоникалықтыларына тең болады

.

Осыған ұқсас реактив қуат үшін жазуға болады:

.

Толық қуат .

Синусоидалы емес ток үшін

70. Кешенді түрдегі Ом заңы

Кирхгофтың теңдеуінде

(6.3)

rLС берілген көрсеткіштер мен синусоидалды кернеу тізбектің қысқыштарындағы ізделінді тоқ өлшемі болсын дерлік. Бұл жерде тізбектегі синусоидалды тоқ құрылым жүйесі болғандықтан, бұл дифферен-циалдық теңдеудің шешімі синусоидалды функция түрінде берілу керек

Кешенді амплитудалық кернеу мен тоқ сәйкесінше тең болады

Теңдеудегі дифференциалдық және интегралдық синусоидалды функ-цияның қосындысын (6.3) кешенді функция сияқты математикалық операция-лармен ауыстырамыз.

Кешенді алгебралық теңдеу, мына түрдегі теңдеуге сәйкес (6.3)

(6.4)

I_m тоғын жақшаның сыртына шығаруға болады. Осыған орай электрлік тізбектегі кешенді кедергіге шартты белгі енгізіледі

(6.5)

Осылай кешенді амплитудалық және әсерлік мәндерін сипаттайтын Ом заңы орындалады

U_m=ZI_m және Ů=Zİ. (6.6)

Кешенді кедергі тригонометриялық және көрсеткішті түрде былай жазылады

Z = zcosφ+jzsinφ

Z= ze^jφ = z<φ (6.8)

мұндағы z – Z кешенді санының модулі және тізбектің толық кедергісі, ал φ – Z кешен санының аргументі

z = φ= arctg (6.9)

(6.6) негізінде тоқтың кешендік амплитудасы:

мұндағы ψ-φ тоқтың бастапқы фазасы. Осыған орай, тригонометриялық түрдегі ізделінген тоқ

i= I_m(İ_m e^jωt)=

6.5 Сурет

6.5 суретте кешендік жазықтық теңдеуінің (6.4) геометриялық түсіндіруі көрсетілген. 6.5,a - сурет тізбектің реактивті кедергісі индуктивтілік сипатқа (x>0) ие болғандағы және φ>0 жағдайға қатысты. 6.5б сурет тізбектің реактивті кедергісі сыйымдылық сипатқа (x>0) (φ<0) ие болғандағы жағдайға қатысты.

6.5 суретте келтірілген векторлық сызбада Ů_r = ri - r кедергідегі кернеу (фаза бойынша I тоғына сәйкес келеді), Ů_L=jωLI – L индуктивтегі кернеу (I тоғын π/2 бұрышқа озады) және U_c=-j1/ωc*İ – C сыйымдылықтағы кернеу (I тоғынан π/2 бұрышқа қалады) U_r,U_L,U_c векторларының геометриялық қосындысы тізбектегі U кернеуін береді.

6.4 Кедергінің, индуктивтіліктің және сыйымдылықтың параллель

қосылуы

Егер параллель қосылған r, L, C (6.6 - сурет) элементтерінен тұратын

u = U_msinωt синусоидалды кернеу тіркелген болса, онда осы тізбекпен өткен синусоидалды тоқ мынаған тең болады

i=i_r+i_L+i_C

6.6 Сурет 6.7 Сурет

r кедергідегі i_r тоғы фаза бойынша U кернеуімен сәйкес келеді, L индуктивтегі i_L тоғы қалса, С сыйымдылықтағы i_С тоғы π/2 бұрышқа озады.

Сондықтан тізбектегі жалпы тоқ мынаған тең

(6.10)

b=b_L-b_c=(1/ωC)-ωC тізбектің реактивті өткізгіштігі деп аталады да, таң-баға байланысты (b>0) индуктивті сипаттама немесе сыйымдылық сипаттама (b<0) болады. g=1/r – активті өткізгіш деп аталады.

Кирхгофтың бірінші заңы бойынша

İ=gŮ+ Ů+jωCŮ=İ_r+İ_L+İ_C (6.11)

мұндағы I_r=gŮ – кедергідегі тоқ (фаза бойынша U кернеумен сәйкес келеді).

İ=- Ů - индуктивтіліктегі тоқ

İ=jωCŮ - сыйымдылықтағы тоқ

Кешенді өткізгіш мынаған тең

Y=g-j( -ωC)=g-jb. (6.12)

Кешенді түрдегі Ом заңының теңдеуі

İ= Y Ů (6.13) Тригонометриялық және көрсеткіш түрдегі кешендік өткізгіш келесідей болады

Y = у cos φ-jsin φ; Y=ye^{-j φ}

мұндағы у – кешенді санының модулі

Y - тізбектің толық өткізгіштігі

φ – Y кешенді санының аргументі

y= (6.14)

Кешенді тоқ мынаған тең

i = yUe^J(-)

Бұл синусоидалды тоққа

i = I_m(İ_me^jω) =yU_msin(ωt + ψ - φ)

сәйкес келеді

6.8 суретте кешенді жазықтық теңдеуiнің геометриялық түсіндірілуі көрсетілген. 6.8,a - сурет тізбектің реактивті өткізгіштігі индуктивтілік сипатта (b>0) болғандағы жағдайға ие болып, сонымен қатар тоқ фаза бойынша кернеуден қалады (φ>0). 6.8, б - сурет тізбектің реактивті өткізгіштігі сыйымдылық сипатқа (b<0) ие болып, тоқ фаза бойынша кернеуден озады (φ < 0).

6.8 Сурет