50. Теңгеру (компенсация) теоремасы.

51. Комплекс түрдегі электр қуаттары.

Кешенді қуат

Активті, реактивті және толық қуатты кернеумен тоқтың кешенді суреттері арқылы табуға болады. 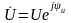болсын, ал . Сонда толық кешенді қуат

(8.11)

- кешенді тоғының түйіндес мәні.

(8.12)

К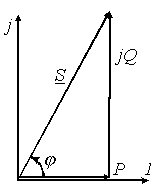 ешенді қуатты қуаттар ұшбұрышына сай қоюға болады (8.4 - суретке қара). 8.4 сурет сай келеді.

52. Комплекс түрдегі Ом және Кирхгоф заңдары.

r, L және С элементтерінің тізбектей қосылуындағы кешенді амплитуда-лық әдістің қолдануын қарастырамыз (6.4 - сурет)

6 .4 Сурет

Кирхгофтың теңдеуінде

(6.3)

rLС берілген көрсеткіштер мен синусоидалды кернеу тізбектің қысқыштарындағы ізделінді тоқ өлшемі болсын дерлік. Бұл жерде тізбектегі синусоидалды тоқ құрылым жүйесі болғандықтан, бұл дифферен-циалдық теңдеудің шешімі синусоидалды функция түрінде берілу керек

Кирхгофтың бірінші заңы бойынша

İ=gŮ+ Ů+jωCŮ=İ_r+İ_L+İ_C (6.11)

мұндағы I_r=gŮ – кедергідегі тоқ (фаза бойынша U кернеумен сәйкес келеді).

İ=- Ů - индуктивтіліктегі тоқ

İ=jωCŮ - сыйымдылықтағы тоқ

Кешенді түрдегі Ом заңының теңдеуі

İ= Y Ů

Y - тізбектің толық өткізгіштігі

53. Тоқ резонансы. Тоқ резонансының қисықтары және сипаттамалары.

Тоқтар резонансы

Параллель тербелмелі контурда тоқтар резонансы мына шартта пайда болады, егер реактивті өткізгіші кіріс болса

; . (12.1)

12.1 Сурет 12.2 Сурет

(12.1) есепке ала отырып, толық өткізгіштің активті екенін анғаруға болады

(12.2)

Тоқтар резонансы жалпы тоқта ең аз және кернеу кірісімен тең (12.2 -сурет)

(12.3)

. (11.4)

Беріктілік контуры

(12.5)

мұндағы -контурдың активті кедергісі;

- өткізу жолағы.

. (12.6)

54. Төртұштылар және олардың негізгі теңдеулері.

Төртұштықтар деп электр энергиясының көзіне және қабылдағышқа қосатын екі қысқышы бар (полюстері), электрлік тізбек немесе оның бөлігін айтамыз. Төртұштықтарға трансформаторлар, күшейткіштер, электрлік сүзгі-лер, электр энергиясын тасымалдайтын желілер және т.б. жатады. Сөйтіп, төртұштықтар теориясы бізге бір тәсілмен құрылымдары және жұмыс істеу принциптері әртүрлі жүйелерді талдауға көмектеседі.

Төртұштықтардың шартты түрде бейнеленуі 14.1.суретте көрсетілген

14.1 Сурет

Қысқыштардың екі буыны 1–1’алғашқылар, қос қысқыштар біріншілік деп аталады, екіншілік деп айтылады, электр энергияның көзі қосылған шықпалар кіріс деп аталады, жүктеме қосылған шықпалар шығыс деп аталады. Тоқтар мен кернеулердің оң бағыттары 14.1.суретте көрсетілген.

Активті және пассивті төртұштықтар.

Активті төртұштықтар тәуелді және тәуелсіз энергия көздері бар, пас-сивті төртұштықтарда жоқ.

Сызықты және сызықсыз төртұштықтар.

Сызықты төртұштықтарда сызықсыз элементтер жоқ, ал сызықсыз төртұштықтарда бар.

Қайтымды және қайтымсыз төртұштықтар.

Қайтымды төртұштықтар үшін қайтымдылық және өзаралық теорема-лары орындалады: кернеудің тоққа кірудегі қатынасы шығуда қысқыштардың орын ауыстырғанда өзгермейді. Пассивті төртұштықтар әрқашан қайтымды.

Симметриялы және симметриясыз төртұштықтар.

Симметриялы төртұштықта кіріс және шығыс қысқыштардың орын ауыстыруы тізбектегі тоқтар мен кернеулерді өзгертпейді.

Типті пассивті төртұштықтар түрлері мына суреттерде көрсетілген: 14.2 а, 14.2 б, 14.2 в, 14.2 г.

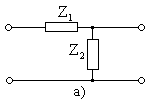
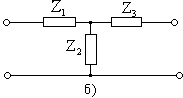
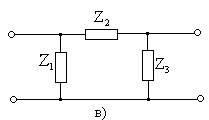
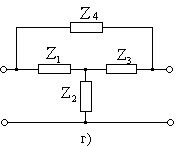
14.2 Сурет

Төртұштықтардың теңдеулері

өзара байланысын анықтайтын теңдеулер төртұштықтардың берілу теңдеулері деп айтылады. Теңдеулерде тоқтар мен кернеулерді байла-ныстыратын шамаларды төртұштықтар көрсеткіштері деп айтады.

Y – типтінің көрсеткіштің берілу теңдеулері

(14.1)

еселеуіштері Y – типті деп айтылады және өткізгіштік мөлшерлігі болады.

Z – типтінің берілу теңдеулері

}. (14.2)

еселеуіштері Z – типті деп айтылады және кедергі өлшемділігіне ие болады.

А- типтінің берілу теңдеулері

}. (14.3)

еселеуіштері А – типті немесе жалпыланған типті деп айтылады. А₁₁,А₂₂ - өлшемсіз, А₁₂ кедергі өлшемділігі бар, А₂₁ өткізгіштік өлшемділігі бар.

Энергияны қысқыштан қысқышқа бергенде қайтымды төрт-ұштықтар теңдеулері А – көрсеткіштері арқылы жазылады және А₁₁ және А₂₂ еселеуіштерінің орындарын ауыстырады.

}. (14.4)

Н – типтінің берілу теңдеулері

}. (14.5)

Y, Z, A, H – көрсеткіштерінің жүйелері көрсеткіш еселеуіштер деп айтылады. Көрсеткіштер – еселеуіштер кешенді шамалар болып табылады. Төртұштықтар сұлбасы және оның элементтері арқылы айқындалады. Әр түрлі көрсеткіштер жүйелерінде көрсеткіш – еселеуіштері арасында байланыс болады. Пассивті төртұштықтар үшін , , А – параметрлері үшін мына қатынас тура

∆А= .

Симметриялы төртұштық үшін А₁₁=А₂₂, Y₁₁=-Y₂₂, Z₁₁=-Z₂₂.