41. Кешенді түрдегі контурлық тоқтар әдісі.

Кирхгоф заңдары

Кирхгофтың бірінші заңы

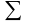İ = 0 (7.1)

Кирхгофтың екінші заңы

Z İ = Ė (7.2)

Мысал. Кирхгофтың заңы бойынша теңдеу құрайық 7.1 – сурет.

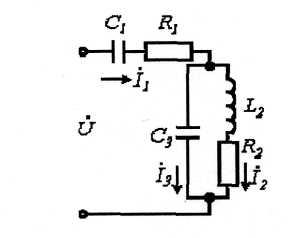
7.1 Сурет

,

,

.

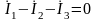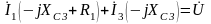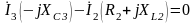7.1.2 Контурлық тоқтар әдісі

Мысал. Контурлық тоқтар әдісі бойынша теңдеу құрайық.

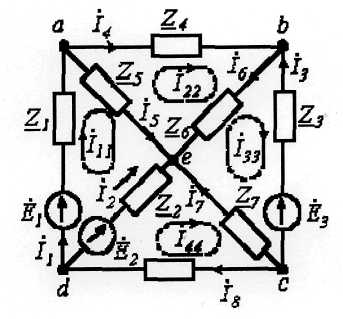
7.2 Сурет

.

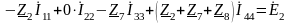Контурлық тоқтар әдісі бойынша және контурдың, тармақтың тоқтарын байланыстыратын теңдеулер арқылы шешеміз

, , , , , , ,

.

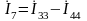42. Векторлы-топографиялық сызба.

Векторлық және топографиялық сызбалары

Синусоидалды түрде өзгеретін ЭҚК-ті, тоқ пен кернеуді кескіндейтін (бейнелейтін) радиус-векторлардың қосындысын векторлық сызба деп атайды. Векторлық сызбалар есептің шығарылуының әрбір қадамын айқын көрсетеді. Векторларды дәл салудың нәтижесінде тікелей осы сызбаның ізделінді амплитудасы мен фазасы анықталынады. Аналитикалық шешу кезінде сызбаны жуық шамасына жақын түрде салу есептеу барысының қадамын сапалы түзетілуін бақылайды.

Тізбектей қосылған элементтері бар тізбектер үшін векторлық сызбаны салған кезде негізгі базалық вектор ретінде тоқтың векторын алған жөн. Элементтері параллель жалғанған тізбектер үшін, негізгі базалық вектор ретінде кернеу векторын алып, оған салыстырмалы түрде параллель тармақтардағы тоқ векторларын бағдарлау керек. Электр тізбегінің әр жеріндегі нүктелерінің арасындағы кернеудің мәні мен фазасын көрнекі түрде анықтау үшін топографиялық сызбаны қолданған тиімді. Олар электр тізбегінің сұлбасына сәйкес жалғанған, олардың потенциялын бейнелейтін, кешенді жазықтықтағы нүктелерді көрсетеді. Өз кезегінде векторлық сызбаны көрсететін топографиялық сызбада кернеу векторының орналасу реті қатаң түрде сұлбадағы элементтердің орналасуымен сәйкес келеді, ал әрбір келесі элементтегі кернеу векторының соңғы жағынан өтеді.

Мысал ретінде тоқтардың векторлық сызбасын және де тізбек үшін потенциалдардың топографиялық сызбасын тұрғызайық

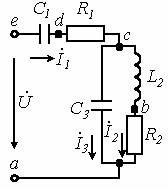
7.4 Сурет

Тізбектің көрсеткіштері

Тізбектің кірісіндегі берілген көрсеткіштер мен кернеулердегі алдын – ала табылған тоқтардың мәндері өзара тең

, , .

Векторлық сызбаны тұрғызу кезінде тоқ және кернеудің масштабтарын береміз (7.5 – суретті қара). Векторлық сызбаны кешенді көрсеткіштік түрде жазылуын, яғни модульдік және фазалық мәндерін біле отырып сала аламыз. Дегенмен практикада алгебралық жазылуын біле отырып сызба тұрғызу анағұрлым ыңғайлы, себебі бұл жағдайда кешендік шаманың нақты және жорамал құраушылары нүктенің кешендік жазықтықтағы орнын анықтай отырып, осы жазықтықтың сәйкес осьтерінде орналасады. Тоқтардың векторлық сызбасы тікелей кешендік шаманың белгілі мәндері арқылы тұрғызылады. Топографиялық сызбаны тұрғызу үшін алдын – ала кешендік потенциалдарды есептейміз (7.4 – сурет). Сұлбадағы әртүрлі потенциалды нүктелерді белгілеп және «а» нүктесіндегі нүктенің потенциалын нөлге тең деп алып, (_а=0) қалған нүктелердің потенциалдарын есептейік

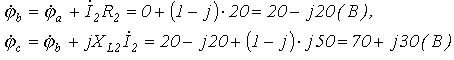
немесе

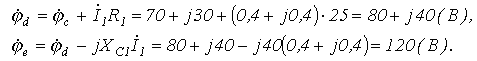
Осылайша, есептеулердің нәтижесі бойынша мынаны алдық , яғни тізбекке қойған U кернеуге тең. Сонымен жүргізілген есептеулер нәтижесінде шықты, бұл тізбектің кірісіндегі U кернеуіне тең. Алынған нәтижелер бойынша топографиялық сызба тұрғызылады (7.5 -сурет). Қорытындылай кетсек, кернеу векторлары топографиялық сызбаның нүктелеріне қатысты электр тізбегіндегі кернеудің оң бағытына қатысты қарама-қарсы бағытталған.

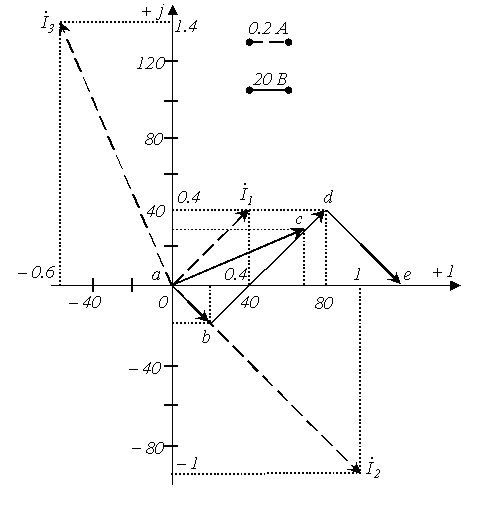
7.5 Сурет